10. 如图,直线a与直线b,c分别交于点A,B,将含45°角的直角三角尺BCD按如图所示放置,∠1= 120°.若要使直线b与直线c平行,可将直线b绕点A逆时针旋转的最小角度为____°.
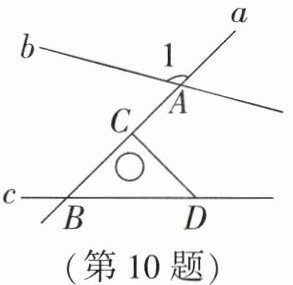
答案:10.15 解析:如图,因为∠1=120°,所以∠2=180°−120°=60°.因为∠ABD=45°,所以当∠2=∠ABD=45°时,b//c,所以直线b绕点A 逆时针旋转至少60°−45°=15°.

11. 新情境 为响应国家新能源建设,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线最大夹角为64°,如图,电池板AB与最大夹角时刻的太阳光线垂直,此时电池板CD与水平线夹角为46°,要使AB//CD,需将电池板CD逆时针旋转m度(0<m<90),则m=
20
.
答案:11.20 解析:因为电池板AB与最大夹角时刻的太阳光线垂直,所以AB与水平线的夹角为90°−64°=26°.要使AB//CD,需令CD与水平线的夹角为26°,所以需将电池板CD逆时针旋转46°−26°=20°.
解析:
解:因为电池板AB与太阳光线垂直,太阳光线与水平线夹角为64°,所以AB与水平线的夹角为90°-64°=26°。要使AB//CD,CD与水平线的夹角需为26°。已知CD初始与水平线夹角为46°,故需逆时针旋转46°-26°=20°。
m=20
12. 如图,在四边形ABCD中,∠ADC+∠ABC= 180°,∠ADF+∠AFD= 90°,点E,F分别在DC,AB上,且BE,DF分别平分∠ABC,∠ADC,判断BE,DF是否平行,并说明理由.

答案:12.BE//DF.理由:因为BE,DF分别平分∠ABC,∠ADC,所以∠ABE=1/2∠ABC,∠ADF=1/2∠ADC.因为∠ADC+∠ABC=180°,所以∠ADF+∠ABE=1/2(∠ADC+∠ABC)=1/2×180°=90°.又因为∠ADF+∠AFD=90°,所以∠ABE=∠AFD,所以BE//DF.
技法点拨
利用同位角判定两直线平行,先找出这两条直线被一条直线所截形成的同位角,再根据题目条件证明这对同位角的数量关系即可.
13. 新趋势 开放性试题 如图,已知∠1= ∠2,有下列条件:①AB⊥BE,CD⊥DF;②BA平分∠EBM,DC平分∠FDM;③BE平分∠ABN,DF平分∠CDN.请你从上述条件中任选一个,试说明:BE//DF.

答案:13.选①.因为AB⊥BE,CD⊥DF,所以∠ABE=∠CDF=90°.
因为∠1=∠2,所以∠1+∠ABE=∠2+∠CDF,即∠EBM=∠FDM.所以BE//DF.
理由:同位角相等,两直线平行
选②.因为BA平分∠EBM,DC平分∠FDM,所以∠EBM=2∠1,∠FDM=2∠2.因为∠1=∠2,所以∠EBM=∠FDM,所以BE//DF.理由:同位角相等,两直线平行
选③.因为BE平分∠ABN,DF平分∠CDN,所以∠EBN=1/2∠ABN,∠FDN=1/2∠CDN.因为∠1=∠2,所以180°−∠1=180°−∠2,即∠ABN=∠CDN,所以∠EBN=∠FDN,所以BE//DF.
理由:同位角相等,两直线平行.
$14. $在同一平面内有$100$条互不重合的直线$,$若$a_1⊥a_2,a_2⊥a_3,a_3⊥a_4,a_4⊥a_5,…,a_{99}⊥a_{100},$则下列结论正确的是$ ($ $)$
A.$a_1//a_{100}$
B.$ a_2⊥a_{98}$
C.$ a_1//a_{99} $
D.$a_{49}//a_{50}$
答案:14.C 解析:可以画图寻找规律,a₁⊥a₂,a₂⊥a₃,a₃⊥a₄,a₄⊥a₅,…,a₉₉⊥a₁₀₀,如图所示(只画出前4条直线).因为∠1=∠2=90°,所以a₁//a₃.又因为∠2=∠3=90°,所以a₂//a₄.以此类推可得a₁//a₃//a₅//…//a₉₉,a₂//a₄//a₆//...//a₁₀₀,所以a₁⊥a₁₀₀,故A错误;a₂//a₉₈,故B错误;a₁//a₉₉,故C正确;a₄₉⊥a₅₀,故D错误.故选C.

15. 如图①,直线EF上有两点A,C,分别引两条射线AB,CD.∠BAF= 110°,CD与AB在直线EF异侧.
(1)若∠DCF= 70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图②,若∠DCF= 60°,射线AB,CD分别绕点A,点C以1°/s和6°/s的速度同时顺时针转动,设时间为t s,在射线CD转动一周的时间内,当时间t的值为____时,CD与AB平行.

答案:15.(1)AB//CD.理由:如图①延长BA至点G,因为∠DCF=70°,所以∠ACD=180°−∠DCF=110°.因为∠BAF=110°,所以∠EAG=∠BAF=110°,所以∠EAG=∠ACD,所以AB//CD.
(2)2或38解析:分三种情况:①如图②,AB与CD在EF的两侧时,因为∠BAF=110°,∠DCF=60°,所以∠ACD=180°−60°−6t°=(120−6t)°,∠BAC=∠EAG=110°−t°.要使AB//CD,则∠ACD=∠EAG,即(120−6t)°=110°−t°,解得t=2.经检验,t=2符合题意.②如图③,CD旋转到与AB都在EF的右侧,即在CD₁ 处时,由题意得∠D₁CF=360°−6t°−60°=(300−6t)°,∠B₁AC=110°−t°.要使AB₁//CD₁,则∠D₁CF=∠B₁AC,即(300−6t)°=110°−t°,解得t=38.经检验,t=38符合题意.③如图④,CD旋转到与AB都在EF的左侧,即在CD₂处时,此时t>110,则6°×110=660°>360°,CD转动超过一周,所以此情况不存在.综上,满足条件的时间t的值为2或38.

技法点拨
解答本题的关键是如何找到相等的同位角,图中EF没有同时去截射线AB,CD时,需要反向延长AB到点G,构造与∠DCF对应的同位角,将角度转化到同一条直线上