1. 如图,已知直线a,b被直线c所截,那么∠1的同位角是 (
D
)
A.∠2
B.∠3
C.∠4
D.∠5
答案:1.D解析:由题图可得,∠1与∠5都在a,b的同侧,并且在第三条直线c(截线)的同旁,所以与∠1构成同位角的是∠5,故选D.
2. (台州中考)如图,已知∠1= 90°,为保证两条铁轨平行,添加的下列条件中,正确的是 (
C
)
A.∠2= 90°
B.∠3= 90°
C.∠4= 90°
D.∠5= 90°
答案:2.C解析:由∠2=90°不能判定两条铁轨平行,所以选项A不符合题意;由∠3=90°=∠1,可判定两枕木平行,所以选项B不符合题意;因为∠1=90°,∠4=90°,所以∠1=∠4,所以两条铁轨平行,所以选项C符合题意;由∠5=90°不能判定两条铁轨平行,所以选项D 不符合题意,故选C.
3. 如图,在∠A,∠B,∠C,∠1,∠2,∠3中,构成同位角的有
∠A和∠1,∠B和∠3,∠C和∠2
.
答案:3.∠A和∠1,∠B和∠3,∠C和∠2 解析:根据同位角的定义可知同位角有∠A和∠1,∠B和∠3,∠C和∠2.
4. (2024·宿迁期中)如图是利用直尺和三角尺过直线l外一点P作直线l的平行线的方法,这样做的依据是
同位角相等,两直线平行
.
答案:4.同位角相等,两直线平行
5. 如图,填空:
(1)若∠D= ∠EFC,则
AD
//
EF
,理由:
同位角相等,两直线平行
.
(2)若∠B= ∠AEF,则
BC
//
EF
,理由:
同位角相等,两直线平行
.
答案:5.(1)AD EF 同位角相等,两直线平行
(2)BC EF 同位角相等,两直线平行
6. 如图,直线EF与直线AB,CD相交于点E,F,GF⊥CD交CD于点F.
(1)若添加一个条件:∠1=
∠EFD
,则AB//CD;
(2)若∠1= 125°,则∠2=
35
°时,AB//CD.
答案:6.(1)∠EFD 解析:∠1与∠EFD是同位角,故当∠1=∠EFD时,AB//CD.
(2)35 解析:要使得AB//CD,则应满足∠EFD=∠1=125°,此时∠EFC=180°−∠EFD=180°−125°=55°.因为GF⊥CD,所以∠CFG=90°,则∠2=180°−∠EFC−∠CFG=180°−55°−90°=35°.
7. 教材P184例1变式 如图,直线AB,CD与GH分别相交于点E,F,EM平分∠BEF,FN平分∠DFH,∠BEF= ∠DFH.指出图中互相平行的直线,并说明理由.
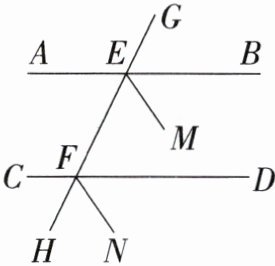
答案:7.AB//CD,EM//FN.理由如下:
因为∠BEF与∠DFH是AB,CD被GH所截形成的同位角,且∠BEF=∠DFH,所以AB//CD.
理由:同位角相等,两直线平行
∠MEF与∠NFH是EM,FN被GH截成的同位角.因为EM平分∠BEF,FN平分∠DFH,所以∠BEF=2∠MEF,∠DFH=2∠NFH.因为∠BEF=∠DFH,所以∠MEF=∠NFH,所以EM//FN.
理由:同位角相等,两直线平行
8. (2024·淄博期中)下列图形中,∠1和∠2不是同位角的是 (
B
)
答案:8.B 解析:由同位角的定义可知,选项B中∠1与∠2的两条边都不在同一条直线上,不是同位角,故选B.
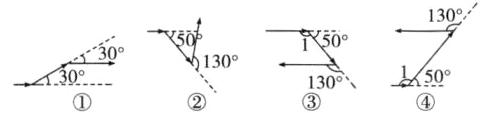
9. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是 ( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向右拐50°,第二次向右拐130°
D.第一次向左拐50°,第二次向左拐130°
答案:9.A 解析:由题意得,汽车两次拐弯前后路线平行且方向相同.根据选项画出对应示意图,如图①②③④.因为图①前后路线显然平行且同向,所以选项A正确;因为图②前后路线显然不同向,且前后路线也不平行,所以选项B错误;因为图③中,∠1=180°−50°=130°,前后路线平行但不同向,所以选项C错误;因为图④中,∠1=180°−50°=130°,前后路线平行但不同向,所以选项D错误.故选A.