9. (2025·赣州月考)在数轴上有间隔相等的四个点M,N,P,Q,所表示的数分别为m,n,p,q,其中有两个数互为相反数,若m的绝对值最大,则数轴的原点是(
D
)
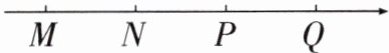
A.点N
B.点P
C.点P或点N,P的中点
D.点P或点P,Q的中点
答案:D 解析:因为$m$的绝对值最大,所以点$M$离原点最远.因为有两个数互为相反数,所以原点在某两点之间线段的中点处,综上,原点是点$P$,$Q$的中点或点$P$.故选D.
10. (1)一个数在数轴上所对应的点向左平移6个单位长度后,得到它的相反数所对应的点,则这个数为
3
.
(2)在数轴上有A,B两点,已知点B对应的数为-2,若将原点O向左移动4个单位长度,A,B两点对应的数恰好互为相反数,则点A原来对应的数是
-6
.
答案:(1)3 解析:互为相反数的两个数表示的点到原点的距离相等,所以该点到原点的距离为3且在原点右侧,故答案为3.
(2)-6 解析:将原点$O$向左移动4个单位长度后,点$B$对应的数变为2,$A$,$B$两点对应的数恰好互为相反数,故此时点$A$对应的数为-2,将原点$O$向右移动4个单位长度,还原到原来位置,此时点$A$对应的数为-6.
11. 化简下列各式的符号,并回答问题:
(1)$-[-(-3)]=$
-3
;
$-[-(+4.5)]=$
4.5
;
$-\{ +[-(+5)]\} =$
5
;
$-\{ -[-(+7)]\} =$
-7
.
(2)当+5前面有99个负号时,化简后的结果是
-5
;当-5前面有100个负号时,化简后的结果是
-5
;你能总结出什么规律?
规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数;一个数的前面有偶数个负号,化简后的结果等于它本身.
(3)计算:
$\underbrace{-(-(-…-(-3)…))}_{2n个负号,n是正整数}+(\underbrace{-(-(-…-(-1)…))}_{(2n - 1)个负号,n是正整数}).$
$\underbrace{-(-(\cdots-(-3)\cdots))}_{2n个负号,n是正整数}+\underbrace{(-(-(\cdots-(-1)\cdots))}_{(2n - 1)个负号,n是正整数}=3 - 1 = 2$
答案:(1)-3 4.5 5 -7
(2)-5 -5 规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数;一个数的前面有偶数个负号,化简后的结果等于它本身.
(3)$\underbrace{-(-(\cdots-(-3)\cdots))}_{2n个负号,n是正整数}+\underbrace{(-(-(\cdots-(-1)\cdots))}_{(2n - 1)个负号,n是正整数}=3 - 1 = 2$
12. 在数轴上点A表示的数是4,点B,C表示互为相反数的两个数,且点C与点A之间的距离为2,求数轴上A,B两点之间的距离.
答案:如图①所示,与点$A$相距2个单位长度的点有两个,分别是数2和数6表示的点,所以点$C$表示的数是2或6.
如图②所示,当点$C$表示的数是2时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-2,此时$A$,$B$两点之间的距离为6.
如图③所示,当点$C$表示的数是6时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-6,此时$A$,$B$两点之间的距离为10.
综上,点$A$与点$B$两点之间的距离为6或10.


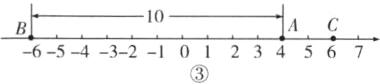
13. 已知表示互为相反数的两个数的点A,B在数轴上的距离是12,将点A沿着数轴先向右运动2s,再向左运动5s到达点C的位置. 设点A的运动速度为每秒1.5个单位长度,则点C表示的数的相反数为
-1.5或10.5
.
答案:-1.5或10.5 解析:因为表示互为相反数的两个数的点$A$,$B$在数轴上的距离是12,所以点$A$在数轴上表示的数为6或-6.注意到$1.5×2 = 3$,$1.5×5 = 7.5$.①当点$A$在数轴上表示的数为6时,先向右运动2s,得数9,再向左运动5s,得数1.5,即点$C$在数轴上表示的数为1.5,它的相反数为-1.5;②当点$A$在数轴上表示的数为-6时,先向右运动2s,得数-3,再向左运动5s,得数-10.5,即点$C$在数轴上表示的数为-10.5,它的相反数为10.5.
解析:
解:因为互为相反数的两个数的点A,B在数轴上距离是12,所以点A表示的数为6或-6。
点A运动速度为每秒1.5个单位长度,运动总时间为2s向右、5s向左,运动后位置变化为:1.5×2 - 1.5×5 = 3 - 7.5 = -4.5(单位长度),即点A最终向左移动4.5个单位长度到点C。
①当点A表示6时,点C表示的数为6 - 4.5 = 1.5,其相反数为-1.5;
②当点A表示-6时,点C表示的数为-6 - 4.5 = -10.5,其相反数为10.5。
-1.5或10.5
14. 已知a为有理数,数轴上表示$-a$与a的点之间(包括$-a$和a)有99个整数点. (“≥”表示“大于或等于”“不小于”;“≤”表示“小于或等于”“不大于”)
(1)$-a$与a互为相反数吗?
(2)在a与$-a$之间,原点的左右两侧各有多少个整数点?
(3)a的取值范围是什么?
答案:(1)$-a$与$a$互为相反数.
(2)$-a$与$a$之间有99个整数点,则原点左右两侧各有$(99 - 1)÷2 = 49$(个)整数点.
(3)$a$对应的点到原点的距离在49到50之间,且不能等于50,则$a$的取值范围是$-50 < a ≤ -49$或$49 ≤ a < 50$.