9. (2025·南京期末)如图,直线AB,CD相交于点O,OE平分$∠BOD,∠AOC+∠DOE= 45^{\circ }$,则$∠COB=$
150
$^{\circ }$.
答案:150 解析:因为 OE 平分 $ \angle BOD $,$ \angle AOC = \angle BOD $,所以 $ \angle DOE = \frac{1}{2} \angle BOD = \frac{1}{2} \angle AOC $。因为 $ \angle AOC + \angle DOE = 45^\circ $,所以 $ \frac{3}{2} \angle BOD = 45^\circ $,所以 $ \angle BOD = 30^\circ $,所以 $ \angle COB = 180^\circ - 30^\circ = 150^\circ $。
解析:
解:∵直线AB,CD相交于点O
∴∠AOC=∠BOD(对顶角相等)
∵OE平分∠BOD
∴∠DOE=∠BOE=$\frac{1}{2}$∠BOD=$\frac{1}{2}$∠AOC
∵∠AOC+∠DOE=45°
∴∠AOC+$\frac{1}{2}$∠AOC=45°,即$\frac{3}{2}$∠AOC=45°
解得∠AOC=30°
∴∠BOD=∠AOC=30°
∵∠COB+∠BOD=180°(邻补角互补)
∴∠COB=180°-∠BOD=180°-30°=150°
150
10. 观察下列各图,寻找对顶角(不含平角).如图①,图中有2条直线相交于一点,则对顶角有
2
对;如图②,图中有3条直线相交于一点,则对顶角有
6
对;如图③,图中有n条直线相交于一点,则对顶角有
$ n(n - 1) $
对(用含n的代数式表示).
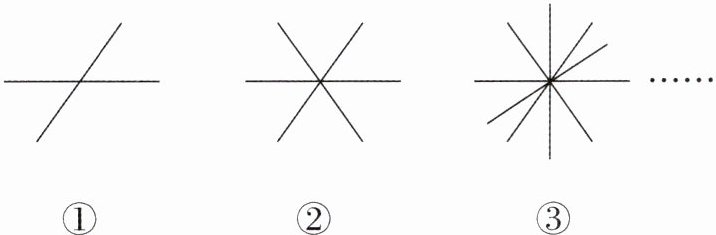
答案:2 6 $ n(n - 1) $ 解析:如题图 ①,图中共有 $ 1 × 2 = 2 $(对)对顶角;如题图 ②,图中共有 $ 2 × 3 = 6 $(对)对顶角;研究题图 ①~题图 ② 中直线条数与对顶角的对数之间的关系,可得若有 n 条直线相交于一点,则可形成 $ [n(n - 1)] $ 对对顶角。
11. 已知直线AB,CD相交于点O,$∠BOD= 70^{\circ }$.
(1)如图①,若$∠AOE= 20^{\circ }$,求$∠COE$的度数.
(2)如图②,若射线OE平分$∠AOC$,画OE的反向延长线OF,OF是否平分$∠BOD$?试说明理由.
(3)在(2)的条件下,以O为顶点,OD为一边画$∠DOG= 90^{\circ }$,求$∠GOF$的度数.

答案:(1) 因为 $ \angle AOC = \angle BOD = 70^\circ $,$ \angle AOE = 20^\circ $,所以 $ \angle COE = \angle AOC - \angle AOE = 70^\circ - 20^\circ = 50^\circ $。
(2) 画出 OE 的反向延长线 OF,如图 ①,OF 平分 $ \angle BOD $。
理由:因为射线 OE 平分 $ \angle AOC $,所以 $ \angle AOE = \angle COE $。
因为 $ \angle AOE = \angle BOF $,$ \angle COE = \angle DOF $,
,所以 $ \angle BOF = \angle DOF $,所以 OF 平分 $ \angle BOD $。

(3) 如图 ①,OG 在 EF 下方时,因为 OF 平分 $ \angle BOD $,所以 $ \angle DOF = \frac{1}{2} \angle BOD = \frac{1}{2} × 70^\circ = 35^\circ $。因为 $ \angle DOG = 90^\circ $,所以 $ \angle GOF = 90^\circ + 35^\circ = 125^\circ $。如图 ②,OG 在 EF 上方时,因为 OF 平分 $ \angle BOD $,所以 $ \angle DOF = \frac{1}{2} \angle BOD = \frac{1}{2} × 70^\circ = 35^\circ $。因为 $ \angle DOG = 90^\circ $,所以 $ \angle GOF = \angle GOD - \angle DOF = 90^\circ - 35^\circ = 55^\circ $。综上所述,$ \angle GOF $ 的度数为 $ 55^\circ $ 或 $ 125^\circ $。
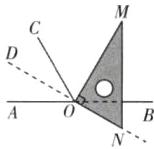
12. 如图①,点O为直线AB上一点,过点O作射线OC,使$∠BOC= 120^{\circ }$.将一直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在$∠BOC$的内部,且恰好平分$∠BOC$.问:此时直线ON是否平分$∠AOC$?请说明理由.
(2)将图①中的三角尺绕点O以每秒$6^{\circ }$的速度沿逆时针方向旋转一周,在旋转的过程中,第t s时,直线ON恰好平分锐角$∠AOC$,求t的值.
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在$∠AOC$的内部,试探索:ON在$∠AOC$的内部旋转时,$∠AOM与∠NOC$的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.

答案:(1) 直线 ON 平分 $ \angle AOC $。理由如下:如图,设 ON 的反向延长线为 OD。因为 OM 平分 $ \angle BOC $,所以 $ \angle MOC = \angle MOB $。又因为 $ \angle MOD = \angle MON = 90^\circ $,所以 $ \angle COD = \angle BON $。又因为 $ \angle AOD = \angle BON $,所以 $ \angle COD = \angle AOD $,所以 OD 平分 $ \angle AOC $,即直线 ON 平分 $ \angle AOC $。
(2) 如图,因为 $ \angle BOC = 120^\circ $,所以 $ \angle AOC = 180^\circ - \angle BOC = 60^\circ $,所以 $ \angle BON = \angle COD = 30^\circ $,即旋转 $ 60^\circ $ 或 $ 240^\circ $ 时直线 ON 平分 $ \angle AOC $。由题意得 $ 6t = 60 $ 或 $ 6t = 240 $,解得 $ t = 10 $ 或 $ t = 40 $。
(3) 不变。因为 $ \angle MON = 90^\circ $,$ \angle AOC = 60^\circ $,所以 $ \angle AOM = 90^\circ - \angle AON $,$ \angle NOC = 60^\circ - \angle AON $,所以 $ \angle AOM - \angle NOC = (90^\circ - \angle AON) - (60^\circ - \angle AON) = 30^\circ $。故 $ \angle AOM $ 与 $ \angle NOC $ 的差不变,且 $ \angle AOM - \angle NOC = 30^\circ $。