1. 教材P172练习T1变式 (2024·北京期中)下列各图中,$∠1和∠2$是对顶角的是 (
D
)
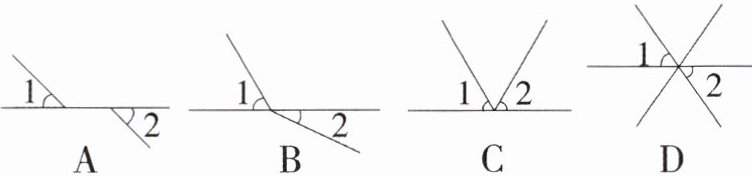
答案:D
解析:
根据对顶角的定义:两条直线相交后所得的只有一个公共顶点且两边互为反向延长线的两个角叫做对顶角。
分析各选项:
选项A:∠1和∠2没有公共顶点,不是对顶角。
选项B:∠1和∠2的两边不互为反向延长线,不是对顶角。
选项C:∠1和∠2的两边不互为反向延长线,不是对顶角。
选项D:∠1和∠2有公共顶点,且两边互为反向延长线,是对顶角。
答案:D
2. 下列说法中正确的是 (
D
)
A.相等的角是对顶角
B.两条直线相交所成的两个角是对顶角
C.有公共顶点,并且相等的角是对顶角
D.对顶角的余角和补角都相等
答案:D
解析:
解:A. 相等的角不一定是对顶角,例如两直线平行时同位角相等,但同位角不是对顶角,故A错误;
B. 两条直线相交所成的邻补角不是对顶角,故B错误;
C. 有公共顶点且相等的角不一定是对顶角,例如角平分线分成的两个角,故C错误;
D. 对顶角相等,所以它们的余角和补角都相等,故D正确。
答案:D
3. 新趋势 跨学科融合 (2025·吉安模拟)光线从空气斜射向水中时会发生折射现象,如图,长

方形ABFE为盛满水的水槽,一束光线从点P射向水面上的点D,折射后照到水槽底部的点C.测得$α=40^{\circ },β=30^{\circ }$,若P,D,B三点在同一条直线上,则$∠BDC$的度数为 (
D
)
A.$40^{\circ }$
B.$30^{\circ }$
C.$20^{\circ }$
D.$10^{\circ }$
答案:D
解析:
解:由题意知,光线从空气斜射向水中,∠α=40°为入射角,∠β=30°为折射角。
因为ABFE是长方形,所以水面EF与底部AB平行,过点D作水面EF的垂线(法线),则法线与EF垂直。
入射角α为入射光线PD与法线的夹角,折射角β为折射光线DC与法线的夹角。
由于P、D、B三点共线,直线PDB与法线的夹角为α=40°,折射光线DC与法线的夹角为β=30°,
所以∠BDC=α - β=40° - 30°=10°。
答案:D
4. 如图,直线a,b相交于点O,将量角器的中心与点O重合,发现表示$60^{\circ }$的点在直线a上,表示$135^{\circ }$的点在直线b上,则$∠1= $
75
$^{\circ }$.

答案:75
解析:
解:由量角器读数可知,直线a对应的刻度为$60^{\circ}$,直线b对应的刻度为$135^{\circ}$。
两刻度差为$135^{\circ}-60^{\circ}=75^{\circ}$,即直线a与直线b的夹角为$75^{\circ}$。
因为$\angle1$是直线a与直线b相交形成的角,所以$\angle1 = 75^{\circ}$。
75
5. (1)如图①,直线AB,CD,EF相交于点O,$∠1= 20^{\circ },∠BOC= 80^{\circ }$,则$∠2$的度数为
$60^\circ$
.
(2)如图②,已知直线AB和CD相交于点O,$∠COE$是直角,OF平分$∠AOE,∠COF= 24^{\circ }$,则$∠BOD$的度数为
42
$^{\circ }$.

答案:(1) $60^\circ$ (2) 42
解析:
(1)
∵∠BOC=80°,∠1=20°,
∴∠BOF=∠BOC - ∠1=80° - 20°=60°,
∵∠2与∠BOF是对顶角,
∴∠2=∠BOF=60°。
(2)
∵∠COE是直角,
∴∠COE=90°,
∵∠COF=24°,
∴∠EOF=∠COE - ∠COF=90° - 24°=66°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=2×66°=132°,
∵∠AOC=∠AOE - ∠COE=132° - 90°=42°,
∵∠BOD与∠AOC是对顶角,
∴∠BOD=∠AOC=42°。
答案:(1)60°;(2)42。
6. 如图,直线AB,CD相交于点O,OE平分$∠AOD,∠FOC= 90^{\circ },∠1= 40^{\circ }$,求$∠2和∠3$的度数.

答案:因为 $ \angle FOC = 90^\circ $,$ \angle 1 = 40^\circ $,AB 为直线,所以 $ \angle 3 + \angle FOC + \angle 1 = 180^\circ $,所以 $ \angle 3 = 180^\circ - 90^\circ - 40^\circ = 50^\circ $。因为 $ \angle AOD $ 和 $ \angle BOC $ 为对顶角,所以 $ \angle AOD = 40^\circ + 90^\circ = 130^\circ $。因为 OE 平分 $ \angle AOD $,所以 $ \angle 2 = \frac{1}{2} \angle AOD = 65^\circ $。
解析:
解:因为 $ \angle FOC = 90^\circ $,$ \angle 1 = 40^\circ $,AB为直线,
所以 $ \angle 3 + \angle FOC + \angle 1 = 180^\circ $,
所以 $ \angle 3 = 180^\circ - \angle FOC - \angle 1 = 180^\circ - 90^\circ - 40^\circ = 50^\circ $。
因为 $ \angle AOD $ 与 $ \angle BOC $ 是对顶角,
且 $ \angle BOC = \angle 1 + \angle FOC = 40^\circ + 90^\circ = 130^\circ $,
所以 $ \angle AOD = \angle BOC = 130^\circ $。
因为 OE 平分 $ \angle AOD $,
所以 $ \angle 2 = \frac{1}{2} \angle AOD = \frac{1}{2} × 130^\circ = 65^\circ $。
综上,$ \angle 2 = 65^\circ $,$ \angle 3 = 50^\circ $。
7. (2024·高密月考)如图,直线AB与CD相交于点O,$∠DOE= α,∠DOF:∠AOD= 2:3$,射线OE平分$∠BOF$,则$∠BOC= $ (
D
)
A.$30^{\circ }$
B.$40^{\circ }$
C.$540^{\circ }-5α$
D.$540^{\circ }-6α$
答案:D 解析:设 $ \angle DOF = 2x $,则 $ \angle AOD = 3x $,所以 $ \angle AOF = 5x $,所以 $ \angle BOF = 180^\circ - 5x $。因为 OE 平分 $ \angle BOF $,所以 $ \angle FOE = \frac{1}{2} \angle BOF = \frac{1}{2}(180^\circ - 5x) = 90^\circ - \frac{5}{2}x $。因为 $ \angle DOE = \alpha $,所以 $ \angle DOF + \angle FOE = \alpha $,即 $ 2x + 90^\circ - \frac{5}{2}x = \alpha $,解得 $ x = 180^\circ - 2\alpha $。则 $ \angle AOD = 3x = 3 × (180^\circ - 2\alpha) = 540^\circ - 6\alpha $,所以 $ \angle BOC = \angle AOD = 540^\circ - 6\alpha $。故选 D。
8. (2024·深圳期中)如图,直线AB,CD相交于点O,$∠AOE= 90^{\circ },∠DOF= 90^{\circ }$,OB平分$∠DOG$,给出下列结论:①当$∠AOF= 60^{\circ }$时,$∠DOE= 60^{\circ }$;②与$∠BOD$相等的角有三个;③OD为$∠EOG$的平分线;④$∠COG= 180^{\circ }-2∠EOF$.其中正确的结论有 (
C
)

A.1个
B.2个
C.3个
D.4个
答案:C 解析:$ \angle AOF + \angle EOF = \angle DOE + \angle EOF = 90^\circ $,因此 $ \angle AOF = \angle DOE $,当 $ \angle AOF = 60^\circ $ 时,$ \angle DOE = 60^\circ $,正确,故 ① 符合题意;OB 平分 $ \angle GOD $,因此 $ \angle GOD = 2 \angle BOD $,而 $ \angle DOE = 90^\circ - \angle BOD $,所以 $ \angle DOE $ 不一定等于 $ \angle GOD $,因此 OD 不一定是 $ \angle EOG $ 的平分线,故 ③ 不符合题意;$ \angle EOF + \angle EOD = \angle BOD + \angle EOD = 90^\circ $,因此 $ \angle EOF = \angle BOD $,由 OB 平分 $ \angle GOD $ 得到 $ \angle GOB = \angle BOD $,又 $ \angle AOC = \angle BOD $,因此与 $ \angle BOD $ 相等的角有三个,正确,故 ② 符合题意;$ \angle COG = \angle AOB - \angle AOC - \angle GOB = \angle AOB - 2 \angle EOF = 180^\circ - 2 \angle EOF $,正确,故 ④ 符合题意。其中正确的结论有 3 个。故选 C。