1. 已知 $ \angle AOB $ 和 $ \angle AOC $ 是同一个平面内的两个角, $ OD $ 是 $ \angle BOC $ 的平分线.
(1) 若 $ \angle AOB = 50^{\circ} $, $ \angle AOC = 70^{\circ} $,分别求出图①,图②中 $ \angle AOD $ 的度数;
(2) 若 $ \angle AOB = m $, $ \angle AOC = n $,其中 $ 0^{\circ} < m < 90^{\circ} $, $ 0^{\circ} < n < 90^{\circ} $, $ m + n < 180^{\circ} $ 且 $ m < n $,直接写出 $ \angle AOD $ 的度数. (结果用含 $ m $, $ n $ 的代数式表示)
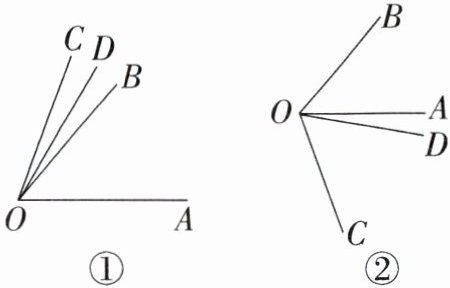
答案:(1) 题图①中,$∠BOC = ∠AOC - ∠AOB = 20^{\circ}$。因为 OD 是$∠BOC$的平分线,所以$∠COD = \frac{1}{2}∠BOC = \frac{1}{2}×20^{\circ} = 10^{\circ}$,所以$∠AOD = ∠AOC - ∠COD = 70^{\circ} - 10^{\circ} = 60^{\circ}$;题图②中,$∠BOC = ∠AOC + ∠AOB = 120^{\circ}$。因为 OD 是$∠BOC$的平分线,所以$∠BOD = \frac{1}{2}∠BOC = \frac{1}{2}×120^{\circ} = 60^{\circ}$,所以$∠AOD = ∠BOD - ∠AOB = 60^{\circ} - 50^{\circ} = 10^{\circ}$。
(2)$∠AOD = \frac{n + m}{2}$或$\frac{n - m}{2}$。解析:如图①,当 OB 在$∠AOC$的内部时,$∠BOC = ∠AOC - ∠AOB = n - m$。因为 OD 是$∠BOC$的平分线,所以$∠BOD = \frac{1}{2}∠BOC = \frac{n - m}{2}$,所以$∠AOD = ∠AOB + ∠BOD = \frac{n + m}{2}$。

如图②,当 OB 在$∠AOC$的外部时,$∠BOC = ∠AOC + ∠AOB = n + m$。因为 OD 是$∠BOC$的平分线,所以$∠BOD = \frac{1}{2}∠BOC = \frac{n + m}{2}$,所以$∠AOD = ∠BOD - ∠AOB = \frac{n - m}{2}$。
方法总结
2. (2024·莆田期末) 如图,过点 $ O $ 在 $ \angle AOB $ 内部作射线 $ OC $. $ OE $, $ OF $ 分别平分 $ \angle AOC $ 和 $ \angle BOC $, $ \angle AOC $ 与 $ \angle AOB $ 互补.
(1) 如图①,若 $ \angle AOC = 70^{\circ} $,求 $ \angle EOF $ 的度数.
(2) 如图②, $ OD $ 平分 $ \angle AOB $.
① 若 $ \angle AOC - 3 \angle COD = 32^{\circ} $,求 $ \angle EOF $ 的度数;
② 试探索:当 $ k $ 为何值时, $ \frac{k \angle AOB - \angle COD}{\angle DOE} $ 的值是一个定值,并求出这个定值.

答案:(1) 因为$∠AOC$与$∠AOB$互补,$∠AOC = 70^{\circ}$,所以$∠AOB = 180^{\circ} - ∠AOC = 180^{\circ} - 70^{\circ} = 110^{\circ}$,所以$∠BOC = ∠AOB - ∠AOC = 110^{\circ} - 70^{\circ} = 40^{\circ}$。因为 OE,OF 分别平分$∠AOC$和$∠BOC$,所以$∠COE = \frac{1}{2}∠AOC = \frac{1}{2}×70^{\circ} = 35^{\circ}$,$∠COF = \frac{1}{2}∠BOC = \frac{1}{2}×40^{\circ} = 20^{\circ}$,所以$∠EOF = ∠COE + ∠COF = 35^{\circ} + 20^{\circ} = 55^{\circ}$。
(2) ① 因为$∠AOC$与$∠AOB$互补,所以$∠AOB = 180^{\circ} - ∠AOC$。又因为 OD 平分$∠AOB$,所以$∠AOD = \frac{1}{2}∠AOB = \frac{1}{2}(180^{\circ} - ∠AOC) = 90^{\circ} - \frac{1}{2}∠AOC$,所以$∠COD = ∠AOC - ∠AOD = ∠AOC - (90^{\circ} - \frac{1}{2}∠AOC) = \frac{3}{2}∠AOC - 90^{\circ}$,所以$∠AOC - 3∠COD = ∠AOC - 3(\frac{3}{2}∠AOC - 90^{\circ}) = 32^{\circ}$,解得$∠AOC = 68^{\circ}$,所以$∠AOB = 180^{\circ} - ∠AOC = 112^{\circ}$,所以$∠BOC = ∠AOB - ∠AOC = 44^{\circ}$。因为 OE,OF 分别平分$∠AOC$和$∠BOC$,所以$∠COE = \frac{1}{2}∠AOC = \frac{1}{2}×68^{\circ} = 34^{\circ}$,$∠COF = \frac{1}{2}∠BOC = \frac{1}{2}×44^{\circ} = 22^{\circ}$,所以$∠EOF = ∠COE + ∠COF = 34^{\circ} + 22^{\circ} = 56^{\circ}$。
② 由①可得$∠AOB = 180^{\circ} - ∠AOC$,$∠COD = \frac{3}{2}∠AOC - 90^{\circ}$,$∠DOE = ∠COE - ∠COD = \frac{1}{2}∠AOC - (\frac{3}{2}∠AOC - 90^{\circ}) = 90^{\circ} - ∠AOC$,所以$\frac{k∠AOB - ∠COD}{∠DOE} = \frac{k(180^{\circ} - ∠AOC) - (\frac{3}{2}∠AOC - 90^{\circ})}{90^{\circ} - ∠AOC} = \frac{90^{\circ}×(2k + 1) - (\frac{3}{2} + k)∠AOC}{90^{\circ} - ∠AOC}$。因为$\frac{k∠AOB - ∠COD}{∠DOE}$的值是一个定值,所以$2k + 1 = \frac{3}{2} + k$,解得$k = \frac{1}{2}$,所以定值为$2k + 1 = 2$。
归纳总结

3. (2025·吉安期末) 如图,以点 $ O $ 为端点按顺时针方向依次作射线 $ OA $, $ OB $, $ OC $, $ OD $, $ OE $,并且使 $ OB $ 是 $ \angle AOC $ 的平分线, $ OD $ 是 $ \angle COE $ 的平分线.
(1) 若 $ \angle AOB = 50^{\circ} $, $ \angle DOE = 30^{\circ} $,求 $ \angle BOD $ 的度数;
(2) 若 $ \angle AOD = 110^{\circ} $, $ \angle BOE = 100^{\circ} $,求 $ \angle BOD $ 的度数;
(3) 当 $ \angle AOD + \angle BOE = n $ 时,求 $ \angle BOD $ 的度数. (用含 $ n $ 的式子表示)

答案:(1) 因为 OB 是$∠AOC$的平分线,所以$∠BOC = ∠AOB = 50^{\circ}$。因为 OD 是$∠COE$的平分线,所以$∠COD = ∠DOE = 30^{\circ}$,所以$∠BOD = ∠BOC + ∠COD = 50^{\circ} + 30^{\circ} = 80^{\circ}$。
(2) 因为 OB 平分$∠AOC$,OD 平分$∠COE$,所以$∠EOD = ∠DOC$,$∠AOB = ∠COB$。设$∠EOD = ∠DOC = x^{\circ}$,则$∠AOB = ∠COB = (100 - 2x)^{\circ}$。因为$∠COD + ∠COB + ∠AOB = 110^{\circ}$,所以$x + 100 - 2x + 100 - 2x = 110$,解得$x = 30$,即$∠EOD = ∠DOC = 30^{\circ}$,所以$∠BOD = ∠BOE - ∠DOE = 100^{\circ} - 30^{\circ} = 70^{\circ}$。
(3) 设$∠AOB = ∠BOC = x$,$∠EOD = ∠DOC = y$,依题意可知$∠AOD = 2x + y$,$∠BOE = x + 2y$。由$∠AOD + ∠BOE = n$,得$3x + 3y = n$,即$x + y = \frac{1}{3}n$,所以$∠BOD = ∠BOC + ∠COD = x + y = \frac{1}{3}n$。