10. 如图,∠BOC与∠AOC互为补角,OD平分∠AOC, ∠BOC = n°,则∠DOB =
90 + $\frac{1}{2}$n
°.(用含n的代数式表示)
答案:(90 + $\frac{1}{2}$n) 解析:因为∠BOC = n°,且∠BOC + ∠AOC = 180°,所以∠AOC = 180° - n°。因为OD平分∠AOC,所以∠COD = $\frac{1}{2}$(180° - n°) = 90° - $\frac{1}{2}$n°,所以∠DOB = ∠BOC + ∠COD = n° + 90° - $\frac{1}{2}$n° = (90 + $\frac{1}{2}$n)°。
11. 如图,∠AOB = 60°, OC是∠AOB的平分线$,OC_1$是∠AOC的平分线$,OC_2$是$∠AOC_1$的平分线,…,OCₙ是$∠AOCₙ₋_1$的平分线,则∠AOCₙ = ____
$\frac{1}{2^{n + 1}}$×60°
.
答案:$\frac{1}{2^{n + 1}}$×60° 解析:因为OC平分∠AOB,所以∠AOC = $\frac{1}{2}$∠AOB。当n = 1时,因为OC₁平分∠AOC,∠AOB = 60°,所以∠AOC₁ = $\frac{1}{2}$∠AOC = $\frac{1}{2}$×$\frac{1}{2}$∠AOB = $\frac{1}{2^2}$×60°。当n = 2时,因为OC₂是∠AOC₁的平分线,所以∠AOC₂ = $\frac{1}{2}$∠AOC₁ = $\frac{1}{2}$×$\frac{1}{2^2}$×60° = $\frac{1}{2^3}$×60°。当n = 3时,因为OC₃是∠AOC₂的平分线,所以∠AOC₃ = $\frac{1}{2}$∠AOC₂ = $\frac{1}{2^4}$×60°,…,所以∠AOCₙ = $\frac{1}{2^{n + 1}}$×60°。
解析:
解:因为OC平分∠AOB,∠AOB=60°,所以∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°。
当n=1时,OC₁平分∠AOC,∠AOC₁=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×$\frac{1}{2}$×60°=$\frac{1}{2^2}$×60°;
当n=2时,OC₂平分∠AOC₁,∠AOC₂=$\frac{1}{2}$∠AOC₁=$\frac{1}{2}$×$\frac{1}{2^2}$×60°=$\frac{1}{2^3}$×60°;
……
以此类推,∠AOCₙ=$\frac{1}{2^{n+1}}$×60°。
$\frac{1}{2^{n+1}}$×60°
12. (2024·南京期末)如图,已知∠AOC = ∠BOD = m°,
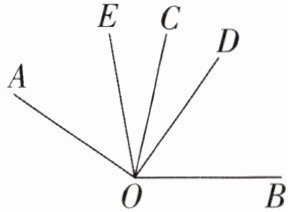
将∠BOD绕点O旋转,使射线OC,OD的夹角为n°,OE平分∠AOD,m + n < 180,m > n,则∠EOC的度数为____°.(用含m,n的代数式表示)
答案:($\frac{1}{2}$m - $\frac{1}{2}$n) 或 ($\frac{1}{2}$m + $\frac{1}{2}$n) 解析:如图①,当OD在∠AOC外部时,由题意可得∠COD = n°,因为∠AOC = m°,所以∠AOD = ∠AOC + ∠COD = m° + n° = (m + n)°。因为OE平分∠AOD,所以∠EOD = $\frac{1}{2}$∠AOD = ($\frac{1}{2}$m + $\frac{1}{2}$n)°,所以∠COE = ∠EOD - ∠COD = ($\frac{1}{2}$m + $\frac{1}{2}$n)° - n° = ($\frac{1}{2}$m - $\frac{1}{2}$n)°。


如图②,当OD在∠AOC内部时,由题意可得∠COD = n°,因为∠AOC = m°,所以∠AOD = ∠AOC - ∠COD = m° - n° = (m - n)°。因为OE平分∠AOD,所以∠EOD = $\frac{1}{2}$∠AOD = ($\frac{1}{2}$m - $\frac{1}{2}$n)°,所以∠COE = ∠EOD + ∠COD = ($\frac{1}{2}$m - $\frac{1}{2}$n)° + n° = ($\frac{1}{2}$m + $\frac{1}{2}$n)°。综上所述,∠EOC的度数为($\frac{1}{2}$m - $\frac{1}{2}$n)°或($\frac{1}{2}$m + $\frac{1}{2}$n)°。
13. 如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗? 为什么?
(2)已知OM平分∠AOC,射线ON在∠COD的内部,且满足∠AOC与∠MON互余.
①若∠AOC = 32°,求∠MON的度数;
②试探究∠AON与∠DON之间的数量关系,请写出结论并说明理由.

答案:(1)∠AOC与∠BOD的度数相等。理由:因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°。因为∠AOC + ∠BOC = 180°,所以∠AOC与∠BOD的度数相等。(2)①因为∠AOC与∠MON互余,所以∠MON = 90° - ∠AOC = 90° - 32° = 58°。②∠AON = ∠DON。理由:如图,因为OM平分∠AOC,所以∠AOC = 2∠AOM,∠COM = ∠AOM。因为∠AOC与∠MON互余,所以∠AOC + ∠MON = 90°,所以∠AON = 90° - ∠AOM,所以∠CON = 90° - 3∠AOM。因为∠BOD与∠BOC互补,所以∠BOD + ∠BOC = 180°,所以∠CON + ∠DON + 2∠BOD = 180°。又因为∠BOD = ∠AOC = 2∠AOM,所以∠DON = 180° - ∠CON - 2∠BOD = 180° - (90° - 3∠AOM) - 4∠AOM = 90° - ∠AOM,所以∠AON = ∠DON。

14. 已知射线OB,OC在∠AOD内部,其中OB为∠AOC的三等分线,OE,OF分别平分∠BOD和∠COD,若∠EOF = 14°,则∠AOC = ____.
答案:84°或42° 解析:因为OB为∠AOC的三等分线,设∠AOC = 3x,则∠BOC = x或2x。因为OF平分∠COD,设∠COD = 2y,则∠DOF = ∠COF = y,那么∠BOD = ∠BOC + ∠COD = x + 2y或2x + 2y。因为OE平分∠BOD,所以∠DOE = ∠BOE = 0.5x + y或x + y,所以∠EOF = ∠DOE - ∠DOF = 0.5x或x。因为∠EOF = 14°,所以x = 28°或14°,所以∠AOC = 3x = 84°或42°。

15. 点O为直线AB上一点,在直线AB同侧任作射线OC,OD,使得∠COD = 90°.
(1)如图①,过点O作射线OE,当OE恰好为∠AOC的平分线时,另作射线OF,使得OF平分∠BOD,则∠EOC + ∠DOF的度数是____°;
(2)如图②,过点O作射线OG,当OG恰好为∠AOD的平分线时,求出∠BOD与∠COG的数量关系;
(3)过点O作射线OH,当OC恰好为∠AOH的平分线时,另作射线OK,使得OK平分∠COD,若∠HOC = 3∠HOK,求出∠AOH的度数.

答案:(1)45 解析:因为OE平分∠AOC,OF平分∠BOD,所以∠EOC = $\frac{1}{2}$∠AOC,∠DOF = $\frac{1}{2}$∠BOD。因为∠COD = 90°,所以∠AOC + ∠BOD = 90°,所以∠EOC + ∠DOF = $\frac{1}{2}$∠AOC + $\frac{1}{2}$∠BOD = 45°。(2)因为OG平分∠AOD,所以∠GOA = ∠GOD = $\frac{1}{2}$∠AOD,根据图形可知∠BOD = 180° - ∠AOD,因为∠COD = 90°,所以∠COG = 90° - ∠GOD = 90° - $\frac{1}{2}$∠AOD。因为∠BOD = 180° - ∠AOD,所以∠BOD = 2∠COG。(3)当OH在OK左侧时,如图①所示。因为∠HOC = 3∠HOK,所以∠KOC = 4∠HOK。因为OK平分∠COD,所以∠KOC = $\frac{1}{2}$∠COD = $\frac{1}{2}$×90° = 45°,所以∠HOK = $\frac{1}{4}$∠KOC = $\frac{45°}{4}$。因为OC平分∠AOH,所以∠AOC = ∠HOC = 3∠HOK = $\frac{135°}{4}$,所以∠AOH = 2∠AOC = 2×$\frac{135°}{4}$ = 67.5°。当OK在OH左侧时,如图②所示。因为∠HOC = 3∠HOK,所以∠KOC = 2∠HOK。因为OK平分∠COD,所以∠KOC = $\frac{1}{2}$∠COD = $\frac{1}{2}$×90° = 45°,所以∠HOK = $\frac{1}{2}$∠KOC = 22.5°。因为OC平分∠AOH,所以∠AOC = ∠HOC = 3∠HOK = 67.5°,所以∠AOH = 2∠AOC = 2×67.5° = 135°。综上所述,∠AOH为135°或67.5°。

