1. (2024·福建期末)已知OC是∠AOB内的一条射线,下列条件中能确定射线OC平分∠AOB的是 (
B
)
A.∠BOC = $\frac{1}{2}$∠AOC
B.∠AOB = 2∠AOC
C.2∠AOC = ∠BOC
D.∠AOB = ∠AOC + ∠BOC
答案:B
解析:
要确定射线OC平分∠AOB,则需满足∠AOC=∠BOC且∠AOC+∠BOC=∠AOB。
对于选项A:∠BOC = $\frac{1}{2}$∠AOC,可得∠AOC=2∠BOC,此时∠AOC≠∠BOC,不符合平分条件。
对于选项B:∠AOB = 2∠AOC,因为∠AOB=∠AOC+∠BOC,所以∠AOC+∠BOC=2∠AOC,即∠BOC=∠AOC,符合平分条件。
对于选项C:2∠AOC = ∠BOC,此时∠AOC≠∠BOC,不符合平分条件。
对于选项D:∠AOB = ∠AOC + ∠BOC,这是角的组成关系,任意射线OC在∠AOB内都满足,不能确定OC平分∠AOB。
综上,能确定射线OC平分∠AOB的条件是选项B。
答案:B
2. (2025·驻马店期末)如图,在O点的观测站测得渔船A位于东北方向,渔船B位于南偏西30°方向,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,则渔船C相对观测站O的方向为 (
A
)
A.南偏东52.5°
B.南偏东37.5°
C.南偏东53.5°
D.南偏东82.5°
答案:A
解析:
解:
∵渔船A位于东北方向,
∴∠AOx=45°(x轴为东方向)。
∵渔船B位于南偏西30°方向,
∴∠BOy=30°(y轴为南方向)。
∠AOB=180°-45°+30°=165°。
∵OC平分∠AOB,
∴∠AOC=165°÷2=82.5°。
∠COx=∠AOC-∠AOx=82.5°-45°=37.5°。
∴渔船C位于南偏东90°-37.5°=52.5°方向。
答案:A
3. 已知∠α = 40.5°, ∠β = 40°50',则∠α
<
∠β.(填“>”“<”或“=”)
答案:<
解析:
解:∠α = 40.5° = 40°30',∠β = 40°50',因为40°30'<40°50',所以∠α<∠β。
<
4. 如图所示,将长方形ABCD的一角沿AE折叠,若∠BAD' = 40°,则∠EAD'的度数为
25°
.
答案:25°
解析:
解:
∵四边形ABCD是长方形,
∴∠DAB=90°。
∵∠BAD'=40°,
∴∠DAD'=∠DAB - ∠BAD'=90° - 40°=50°。
由折叠性质得∠DAE=∠D'AE,
∴∠EAD'=∠DAD'÷2=50°÷2=25°。
25°
5. 如图,点A,O,B在一条直线上,∠AOE = ∠COD, ∠EOD = 30°, OC平分∠EOB,则∠BOC = ____°.
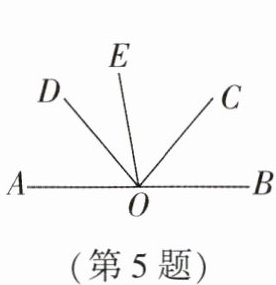
50
答案:50 解析:因为∠AOE = ∠COD,所以∠AOE - ∠DOE = ∠COD - ∠DOE,即∠AOD = ∠COE。因为OC平分∠BOE,所以∠BOC = ∠COE,所以∠BOC = ∠COE = ∠AOD。设∠BOC = ∠COE = ∠AOD = x°,所以3x + 30 = 180,解得x = 50,所以∠BOC = 50°。
6. 如图.
(1)用圆规、直尺作出∠AOB,使∠AOB = ∠α;
(2)反向延长OB到点C,分别用量角器画出∠AOB,∠AOC的平分线OE,OF.(不写作法)

答案:(1)如图①、图②。


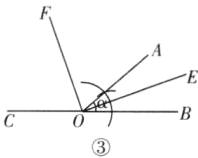
(2)如图③,OE,OF即为所求。
7. 如图,直线AB,CD相交于点O,∠2 - ∠1 = 15°, ∠3 = 130°.
(1)求∠2的度数;
(2)试说明OE平分∠COB.

答案:(1)因为∠3 = 130°,∠1 + ∠3 = 180°,所以∠1 = 180° - ∠3 = 180° - 130° = 50°。因为∠2 - ∠1 = 15°,所以∠2 = 15° + ∠1 = 15° + 50° = 65°。(2)因为∠1 = 50°,∠2 = 65°,∠1 + ∠COE + ∠2 = 180°,所以∠COE = 180° - ∠1 - ∠2 = 65°,所以∠COE = ∠2,所以OE平分∠COB。
8. 如图,已知ON,OM分别平分∠AOC和∠BON.若∠MON = 20°, ∠AOM = 35°,则∠AOB的度数为 (
C
)
A.15°
B.40°
C.55°
D.70°
答案:C 解析:因为ON平分∠AOC,OM平分∠BON,所以∠AON = ∠NOC = $\frac{1}{2}$∠AOC,∠BOM = ∠NOM = $\frac{1}{2}$∠BON。因为∠MON = 20°,∠AOM = 35°,所以∠AON = ∠AOM - ∠MON = 35° - 20° = 15°,所以∠AOC = 2×15° = 30°,∠BOM = ∠NOM = 20°,所以∠AOB = ∠BOM + ∠MON + ∠AON = 20° + 20° + 15° = 55°,故选C。
9. 如图,已知O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,若OC是∠MOB的平分线,则下列结论正确的是 (
B
)
A.∠AOM = 3∠NOC
B.∠AOM = 2∠NOC
C.2∠AOM = 3∠NOC
D.3∠AOM = 5∠NOC
答案:B 解析:因为∠MON = 90°,所以∠AOM = 90° - ∠BON,所以2∠BON = 180° - 2∠AOM。因为OC平分∠BOM,所以∠MOC = ∠BOC = $\frac{1}{2}$∠MOB,所以∠AOM = 180° - 2∠BOC = 180° - 2∠BON - 2∠CON,所以∠AOM = 180° - (180° - 2∠AOM) - 2∠CON,所以∠AOM = 2∠CON。故选B。