10. 如图所示,已知$∠AOC= ∠BOD= 80^{\circ}$,$∠BOC= 30^{\circ}$,则$∠AOD$的度数为
130°
.
答案:130° 解析:因为∠AOC=80°,∠BOC=30°,所以∠AOB=∠AOC−∠BOC=80°−30°=50°,所以∠AOD=∠AOB+∠BOD=50°+80°=130°。
11. 若$∠α=22^{\circ}15',∠β满足3∠α-∠β= 180^{\circ}-3∠β$,则$∠β=$
56°37′30''
.
答案:56°37′30''
解析:
解:由题意得,$3∠α - ∠β = 180^{\circ} - 3∠β$,
移项可得:$3∠β - ∠β = 180^{\circ} - 3∠α$,
即$2∠β = 180^{\circ} - 3∠α$,
因为$∠α = 22^{\circ}15'$,
所以$3∠α = 3×22^{\circ}15' = 66^{\circ}45'$,
则$2∠β = 180^{\circ} - 66^{\circ}45' = 113^{\circ}15'$,
所以$∠β = 113^{\circ}15'÷2 = 56^{\circ}37'30''$。
$56^{\circ}37'30''$
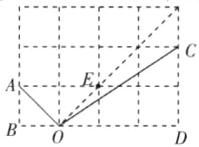
12. (2024·仪征期末)小正方形网格如图所示,点A,B,C,D,O均为格点,那么$∠AOB$______$∠COD$.(填“>”“<”或“=”)
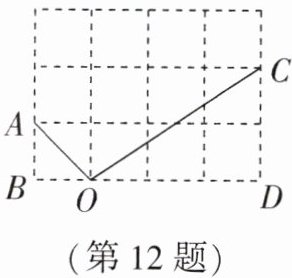
答案:>解析:如图,取格点E,使OA=OE,作射线OE,根据网格特点,易得∠AOB=∠DOE,因为∠DOE>∠COD,所以∠AOB>∠COD
13. 观察下图,回答下列问题:
(1)如图①,在$∠AOB$内部画1条射线OC,则图中有
3
个不同的角;
(2)如图②,在$∠AOB$内部画2条射线OC,OD,则图中有
6
个不同的角;
(3)如图③,在$∠AOB$内部画3条射线OC,OD,OE,则图中有
10
个不同的角;
(4)在$∠AOB$内部画10条射线OC,OD,OE,…,则图中有
66
个不同的角;
(5)在$∠AOB$内部画n条射线OC,OD,OE,…,则图中有
$\frac{(n+1)(n+2)}{2}$
个不同的角.
答案:(1)3 (2)6 (3)10 (4)66 (5)$\frac{(n+1)(n+2)}{2}$解析:在∠AOB内部画n条射线OC,OD,OE,…,则图中有1+2+3+…+n+(n+1)=$\frac{(n+1)(n+2)}{2}$(个)不同的角,故答案为$\frac{(n+1)(n+2)}{2}$。
解析:
(1)3
(2)6
(3)10
(4)66
(5)$\frac{(n+1)(n+2)}{2}$
14. 以$∠AOB$的顶点O为端点引射线OC,使$∠AOC:∠BOC= 5:4$,若$∠AOB= 27^{\circ}$,求$∠AOC$的度数.(本题中的角均为小于$180^{\circ}$的角)
答案:①如图①,当射线OC在∠AOB的内部时,设∠AOC=5x,∠BOC=4x,因为∠AOB=∠AOC+∠BOC=27°,所以5x+4x=27°,解得x=3°,所以∠AOC=15°。


②如图②,当射线OC在∠AOB的外部时,设∠AOC=5x,∠BOC=4x,因为∠AOC=∠AOB+∠BOC,∠AOB=27°,所以5x=27°+4x,解得x=27°,所以∠AOC=135°。 故∠AOC的度数为15°或135°。
15. (1)中午12点15分时,钟表上的时针和分针所成的较小角是
82.5
$^{\circ}$.
(2)在2点到4点之间,时针和分针的夹角会有成$90^{\circ}$的情形,则满足条件的时间点一共有
3
个.
答案:(1)82.5 解析:因为钟表上一共有12个大格,所以每个大格30°。因为时针在钟面上每分钟转0.5°,分针每分钟转6°,所以12点15分时,时针指向12与1之间,分针指向3,所以分针与时针的夹角(较小角)是6°×15−0.5°×15=82.5°。 (2)3 解析:2时和3时之间时,设2时x分,时针和分针的夹角会成90°,则6x−(60+0.5x)=90或6x−(60+0.5x)=270,解得x=$\frac{300}{11}$或x=60(舍去),即2时$\frac{300}{11}$分时,时针和分针的夹角会成90°;3时整,时针与分针的夹角为90°;3时和4时之间时,设3时x分,时针和分针的夹角会成90°,则6x−(90+0.5x)=90,解得x=$\frac{360}{11}$,即3时$\frac{360}{11}$分时,时针和分针的夹角会成90°。综上,2时$\frac{300}{11}$分或3时整或3时$\frac{360}{11}$分时,时针和分针的夹角会成90°。故有3个时间点。
解析:
(1)82.5
解:钟表每个大格30°,时针每分钟转0.5°,分针每分钟转6°。
12点15分时,分针位置:6°×15=90°,
时针位置:0.5°×15=7.5°,
较小夹角:90°-7.5°=82.5°。
(2)3
解:
①2点到3点间:设2时x分夹角90°,
6x - (60 + 0.5x) = 90 或 6x - (60 + 0.5x) = 270,
解得x=300/11(x=60舍去),即2时300/11分;
②3点整:时针与分针夹角90°;
③3点到4点间:设3时x分夹角90°,
6x - (90 + 0.5x) = 90,解得x=360/11,即3时360/11分。
综上,共3个时间点。
16. 图①是由一副三角尺拼成的图案,根据图中提供的信息,解答下列问题:
(1)图①中,$∠EBC$的度数为______
150°
.
(2)能否将图①中的三角尺ABC绕点B逆时针旋转α度$(0^{\circ}<α<90^{\circ}$,如图②),使旋转后的$∠ABE= 2∠DBC$?若能,求出α的度数;若不能,请说明理由.
能。第一种情况:若逆时针旋转α度(0°<α<60°),根据题意得90°−α=2(60°−α),得α=30°;第二种情况,若逆时针旋转α度(60°≤α<90°),根据题意得90°−α=2(α−60°),得α=70°,故α为30°或70°。
(3)能否将图①中的三角尺ABC绕点B顺时针旋转α度$(0^{\circ}<α<90^{\circ}$,如图③),使旋转后的$∠ABE= 2∠DBC$?请直接回答,不必说明理由.
不能
答案:(1)150°解析:∠EBC=∠ABC+∠EBD=60°+90°=150°。 (2)能。第一种情况:若逆时针旋转α度(0°<α<60°),根据题意得90°−α=2(60°−α),得α=30°;第二种情况,若逆时针旋转α度(60°≤α<90°),根据题意得90°−α=2(α−60°),得α=70°,故α为30°或70°。 (3)不能。解析:理由如下:若顺时针旋转α度,根据题意得90°+α=2(60°+α),得α=−30°。因为0°<α<90°,所以α=−30°不符合题意,故不能。
解析:
(1)150°
(2)能。
第一种情况:0°<α<60°时,90°-α=2(60°-α),解得α=30°;
第二种情况:60°≤α<90°时,90°-α=2(α-60°),解得α=70°;
故α为30°或70°。
(3)不能