1. 下列说法中正确的是 (
C
)
A.两条射线组成的图形叫作角
B.有公共端点的两条线段组成的图形叫作角
C.角可以看作是由一条射线绕着它的端点旋转而形成的图形
D.角的边越长,角越大
答案:C
2. 下列各角中,为锐角的是 (
B
)
A.$\frac{1}{2}$平角
B.$\frac{1}{5}$周角
C.$\frac{3}{2}$直角
D.$\frac{1}{2}$周角
答案:B
解析:
解:
A. $\frac{1}{2}$平角 = $\frac{1}{2} × 180^\circ = 90^\circ$,为直角;
B. $\frac{1}{5}$周角 = $\frac{1}{5} × 360^\circ = 72^\circ$,为锐角;
C. $\frac{3}{2}$直角 = $\frac{3}{2} × 90^\circ = 135^\circ$,为钝角;
D. $\frac{1}{2}$周角 = $\frac{1}{2} × 360^\circ = 180^\circ$,为平角。
答案:B
3. (2024·广西中考改编)2时整,钟表的时针和分针所成的锐角为 (
C
)
A.$20^{\circ}$
B.$40^{\circ}$
C.$60^{\circ}$
D.$80^{\circ}$
答案:C
解析:
解:钟表一圈为$360^{\circ}$,共12个大格,每个大格的度数为$360^{\circ}÷12 = 30^{\circ}$。2时整,时针指向2,分针指向12,中间有2个大格,所以所成锐角为$2×30^{\circ}=60^{\circ}$。
答案:C
4. 如图,能用一个字母表示的角为
∠B
;用三个大写字母表示$∠1$为
∠MCB(或∠BCM或∠MCN或∠NCM)
;$∠2$为
∠AMC(或∠CMA)
;$∠3$为
∠CAN(或∠NAC)
.
答案:∠B ∠MCB(或∠BCM或∠MCN或∠NCM) ∠AMC(或∠CMA) ∠CAN(或∠NAC)
5. 把$31^{\circ}12'36''$化为以度为单位是
31.21°
;把$2700''$化为以度为单位是
0.75°
;把$15.81^{\circ}$化为以度分秒为单位是
15°48'36''
.
答案:31.21° 0.75° 15°48'36''
解析:
解:
1. $36'' = 36 ÷ 60 = 0.6'$,$12' + 0.6' = 12.6'$,$12.6' = 12.6 ÷ 60 = 0.21^{\circ}$,$31^{\circ} + 0.21^{\circ} = 31.21^{\circ}$
2. $2700'' = 2700 ÷ 60 = 45'$,$45' = 45 ÷ 60 = 0.75^{\circ}$
3. $0.81^{\circ} = 0.81 × 60 = 48.6'$,$0.6' = 0.6 × 60 = 36''$,所以$15.81^{\circ} = 15^{\circ}48'36''$
31.21°;0.75°;15°48'36''
6. 教材P164练习T3变式 计算:
(1)$153^{\circ}19'42''+26^{\circ}40'28''$;
(2)$108^{\circ}18'-52^{\circ}30''$;
(3)$90^{\circ}3''-57^{\circ}21'44''$.
答案:(1)180°10'' (2)56°17′30'' (3)32°38′19''
解析:
(1)解:$153^{\circ}19'42'' + 26^{\circ}40'28''$
$=(153^{\circ} + 26^{\circ}) + (19' + 40') + (42'' + 28'')$
$=179^{\circ} + 59' + 70''$
$=179^{\circ} + 59' + 1'10''$
$=179^{\circ} + 60' + 10''$
$=180^{\circ}10''$
(2)解:$108^{\circ}18' - 52^{\circ}30''$
$=108^{\circ}17'60'' - 52^{\circ}0'30''$
$=(108^{\circ} - 52^{\circ}) + (17' - 0') + (60'' - 30'')$
$=56^{\circ} + 17' + 30''$
$=56^{\circ}17'30''$
(3)解:$90^{\circ}3'' - 57^{\circ}21'44''$
$=89^{\circ}59'63'' - 57^{\circ}21'44''$
$=(89^{\circ} - 57^{\circ}) + (59' - 21') + (63'' - 44'')$
$=32^{\circ} + 38' + 19''$
$=32^{\circ}38'19''$
7. 某校的升旗台设在校园中心O点,学校生物园A位于O点的东北方向,教学楼B位于O点的南偏东$60^{\circ}$方向,请在图中画出射线OA,OB,并计算$∠AOB$的度数.
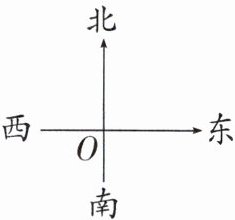
答案:根据题意画图如图: 因为A位于O点的东北方向,所以∠1=45°。因为B位于O点的南偏东60°方向,所以∠2=60°,所以∠AOB=180°−∠1−∠2=180°−45°−60°=75°。

8. (2024·盐城期末)如图,下列各个图形中,能用$∠1,∠AOB,∠O$三种方法表示同一个角的图形是 (
C
)

答案:C
解析:
选项A:以O为顶点的角有多个,不能用∠O表示,故A错误;
选项B:∠1的顶点不是O,不能用∠AOB、∠O表示,故B错误;
选项C:∠1、∠AOB、∠O表示同一个角,故C正确;
选项D:以O为顶点的角有多个,不能用∠O表示,故D错误。
答案:C
9. 已知$∠α,∠β$都是钝角,甲、乙、丙、丁四个同学计算$\frac{1}{6}(∠α+∠β)$的结果依次为28°,48°,60°,88°,其中只有一个同学的计算结果是正确的,则计算出正确结果的是 (
B
)
A.甲
B.乙
C.丙
D.丁
答案:B 解析:因为∠α,∠β都是钝角,所以90°<∠α<180°,90°<∠β<180°,所以180°<∠α+β<360°,从而30°<$\frac{1}{6}$(∠α+∠β)<60°,对比甲、乙、丙、丁的计算结果可知,只有乙的结果符合。