10. 如图,点 $ C,D $ 为线段 $ AB $ 上两点, $ AC + BD = a $,若 $ AD + BC = \frac{7}{5}AB $,用含 $ a $ 的式子表示 $ CD $ 的长为 (
B
)
A.$ \frac{2}{5}a $
B.$ \frac{2}{3}a $
C.$ \frac{5}{3}a $
D.$ \frac{5}{7}a $
答案:B 解析:因为$AD + BC = \frac{7}{5}AB$,所以$AC + CD + CD + DB = \frac{7}{5}(AC + CD + DB)$。因为$AC + BD = a$,所以$a + 2CD = \frac{7}{5}(a + CD)$,所以$CD = \frac{2}{3}a$。故选B。
11. (2025·宁波期末)已知点 $ C $ 是线段 $ AB $ 的中点,点 $ D $ 分线段 $ AB $ 的长度为 $ 5:3 $.已知 $ CD = 7cm $,则 $ AD $ 的长为______ $ cm $.
答案:35或21 解析:因为点C是线段AB的中点,所以$AC = \frac{1}{2}AB$。因为点D分线段AB的长度为$5:3$。当$AD:DB = 5:3$时,如图①,所以此时AD占AB的$\frac{5}{5 + 3} = \frac{5}{8}$,即$AD = \frac{5}{8}AB$,所以$CD = AD - AC = \frac{5}{8}AB - \frac{1}{2}AB = \frac{1}{8}AB$。因为$CD = 7cm$,所以$AB = 7×8 = 56(cm)$,所以$AD = \frac{5}{8}AB = \frac{5}{8}×56 = 35(cm)$。
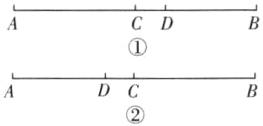
当$AD:DB = 3:5$时,如图②,此时AD占AB的$\frac{3}{3 + 5} = \frac{3}{8}$,即$AD = \frac{3}{8}AB$,所以$CD = AC - AD = \frac{1}{2}AB - \frac{3}{8}AB = \frac{1}{8}AB$。因为$CD = 7cm$,所以$AB = 7×8 = 56(cm)$,所以$AD = \frac{3}{8}AB = \frac{3}{8}×56 = 21(cm)$。故答案为35或21。易错提醒求线段的长时,如果题目中没有给出图形,那么一定要画出所有可能的图形,分情况讨论去计算,以防漏解。本题中需对点D的位置进行分类讨论。
12. 新题型 双空题 有一无弹性细线,拉直时测得细线 $ OP $ 长为 $ 8cm $,现进行如下操作:①在细线上任取一点 $ A $;②将细线折叠,使点 $ O $ 与点 $ A $ 重合,记折点为点 $ B $;③将细线折叠,使点 $ P $ 与点 $ A $ 重合,记折点为点 $ C $.

(1) 如图, $ BC $ 的长为______ $ cm $;
(2) 继续进行折叠,使点 $ B $ 与点 $ C $ 重合,并把点 $ B $ 和与其重叠的点 $ C $ 处的细线剪开,使细线分成长为 $ a,b,c $ 的三段 $ (a < b < c) $, 若 $ a:b = 1:3 $, 则细线未剪开时 $ OA $ 的长为______ $ cm $.
(1)
4
(2)
2或6
答案:(1)4 (2)2或6 解析:因为$a < b < c$,细线剪开后分成OB,BC,CP三段,所以$BC = c$。当$OB = a$时,$CP = b$,因为$OB + CP = 8 - 4 = 4(cm)$,所以$a + b = 4cm$。因为$a:b = 1:3$,所以$a = 1cm$,$b = 3cm$,所以$OA = 2a = 2cm$;当$OB = b$时,$CP = a$,因为$OB + CP = 8 - 4 = 4(cm)$,所以$a + b = 4cm$。因为$a:b = 1:3$,所以$a = 1cm$,$b = 3cm$,所以$OA = 2b = 6cm$。故答案为2或6。
解析:
(1) 4
(2) 解:由题意,细线剪开后分成OB,BC,CP三段,且BC=4cm。
情况一:OB=a,CP=b。
因为OB+CP=8-4=4cm,a:b=1:3,
设a=x,b=3x,则x+3x=4,解得x=1。
所以a=1cm,OA=2OB=2×1=2cm。
情况二:OB=b,CP=a。
因为OB+CP=8-4=4cm,a:b=1:3,
设a=x,b=3x,则x+3x=4,解得x=1。
所以b=3cm,OA=2OB=2×3=6cm。
综上,OA的长为2或6cm。
答案:(1)4;(2)2或6
13. 如图,线段 $ AB = 20cm $,线段 $ AB $ 上有一点 $ C $, $ BC:AC = 1:4 $,点 $ D $ 是线段 $ AB $ 的中点,点 $ E $ 是线段 $ AC $ 的中点.求:
(1) 线段 $ AC $ 的长度;
(2) 线段 $ DE $ 的长度.

答案:(1)因为$AB = 20cm$,$BC:AC = 1:4$,所以$BC = \frac{1}{1 + 4}AB = \frac{1}{5}AB = 4cm$,$AC = 16cm$。(2)因为点D是线段AB的中点,所以$BD = \frac{1}{2}AB = \frac{1}{2}×20 = 10(cm)$,所以$CD = BD - BC = 10 - 4 = 6(cm)$。因为点E是线段AC的中点,所以$CE = \frac{1}{2}AC = \frac{1}{2}×16 = 8(cm)$,所以$DE = CE - CD = 8 - 6 = 2(cm)$。
14. 如图, $ C $ 为线段 $ AB $ 上一点, $ D $ 在线段 $ AC $ 上,且 $ AD = \frac{2}{3}AC $, $ E $ 为线段 $ BC $ 的中点.
(1) 若 $ AC = 6 $, $ BE = 1 $,求线段 $ AB,DE $ 的长;
(2) 试说明: $ AB + BD = 4DE $.

答案:(1)因为E为线段BC的中点,$BE = 1$,所以$BC = 2BE = 2$,$CE = BE = 1$。因为$AC = 6$,所以$AB = AC + BC = 6 + 2 = 8$。因为$AD = \frac{2}{3}AC$,$AC = 6$,所以$AD = 4$,所以$DC = AC - AD = 6 - 4 = 2$,所以$DE = DC + CE = 2 + 1 = 3$。(2)因为$AB = AC + BC$,$BD = BC + CD$,所以$AB + BD = AC + BC + BC + CD$。因为$AD = \frac{2}{3}AC$,E为线段BC的中点,所以$AC = 3CD$,$BC = 2CE$,所以$AB + BD = AC + BC + BC + CD = 3CD + 2CE + 2CE + CD = 4CD + 4CE = 4(CD + CE) = 4DE$。
解析:
(1)
∵E为线段BC的中点,BE=1,
∴BC=2BE=2×1=2,CE=BE=1。
∵AC=6,
∴AB=AC+BC=6+2=8。
∵AD=2/3AC,AC=6,
∴AD=2/3×6=4,
∴DC=AC-AD=6-4=2,
∴DE=DC+CE=2+1=3。
(2)
∵AB=AC+BC,BD=BC+CD,
∴AB+BD=AC+BC+BC+CD。
∵AD=2/3AC,
∴AC=3CD。
∵E为线段BC的中点,
∴BC=2CE。
∴AB+BD=3CD+2CE+2CE+CD=4CD+4CE=4(CD+CE)=4DE。
即AB+BD=4DE。
15. 新题型 新定义 如图①,点 $ C $ 在线段 $ AB $ 上,图中共有 3 条线段: $ AB,AC $ 和 $ BC $, 若其中有一条线段的长度是另一条线段长度的两倍,则称点 $ C $ 是线段 $ AB $ 的“二倍点”.
(1) 一条线段的中点
是
这条线段的“二倍点”.(填“是”或“不是”)
(2) 如图②,点 $ A $ 表示数 $ -10 $,点 $ B $ 表示数 $ 20 $.若点 $ M $ 从点 $ B $ 的位置开始,以每秒 $ 3cm $ 的速度向点 $ A $ 运动,当点 $ M $ 到达点 $ A $ 时停止运动.设运动的时间为 $ t s $.
① 点 $ M $ 在运动的过程中表示的数为
$20 - 3t$
(用含 $ t $ 的式子表示).
② 求 $ t $ 为何值时,点 $ M $ 是线段 $ AB $ 的“二倍点”.
③ 若点 $ M $ 运动的同时点 $ N $ 从点 $ A $ 的位置开始,以每秒 $ 2cm $ 的速度向点 $ B $ 运动,并与点 $ M $ 同时停止.请直接写出点 $ M $ 是线段 $ AN $ 的“二倍点”时 $ t $ 的值.

②当$AM = 2BM$时,$30 - 3t = 2×3t$,解得$t = \frac{10}{3}$;当$AB = 2AM$时,$30 = 2×(30 - 3t)$,解得$t = 5$;当$BM = 2AM$时,$3t = 2×(30 - 3t)$,解得$t = \frac{20}{3}$。综上,t为$\frac{10}{3}$或5或$\frac{20}{3}$时,点M是线段AB的“二倍点”。
③t为$\frac{15}{2}$或$\frac{90}{13}$或$\frac{90}{11}$。
答案:(1)是 (2)①$20 - 3t$ ②当$AM = 2BM$时,$30 - 3t = 2×3t$,解得$t = \frac{10}{3}$;当$AB = 2AM$时,$30 = 2×(30 - 3t)$,解得$t = 5$;当$BM = 2AM$时,$3t = 2×(30 - 3t)$,解得$t = \frac{20}{3}$。综上,t为$\frac{10}{3}$或5或$\frac{20}{3}$时,点M是线段AB的“二倍点”。③t为$\frac{15}{2}$或$\frac{90}{13}$或$\frac{90}{11}$。解析:当$AN = 2MN$时,$2t = 2[2t - (30 - 3t)]$,解得$t = \frac{15}{2}$;当$AM = 2NM$时,$30 - 3t = 2[2t - (30 - 3t)]$,解得$t = \frac{90}{13}$;当$MN = 2AM$时,$2t - (30 - 3t) = 2(30 - 3t)$,解得$t = \frac{90}{11}$。综上,t为$\frac{15}{2}$或$\frac{90}{13}$或$\frac{90}{11}$时,点M是线段AN的“二倍点”。
解析:
(1)是
(2)①$20 - 3t$
②解:由题意,$AB$的长度为$20 - (-10) = 30$,设运动时间为$t$秒,$BM = 3t$,$AM = AB - BM = 30 - 3t$。
当$AM = 2BM$时,$30 - 3t = 2×3t$,解得$t = \frac{10}{3}$;
当$AB = 2AM$时,$30 = 2×(30 - 3t)$,解得$t = 5$;
当$BM = 2AM$时,$3t = 2×(30 - 3t)$,解得$t = \frac{20}{3}$。
综上,$t$为$\frac{10}{3}$或$5$或$\frac{20}{3}$时,点$M$是线段$AB$的“二倍点”。
③$t$为$\frac{15}{2}$或$\frac{90}{13}$或$\frac{90}{11}$。