1. 下列说法正确的是 (
B
)
A.线段的中点可以有两个
B.线段的中点到线段两个端点的距离相等
C.到线段两个端点距离相等的点叫做线段的中点
D.若 $ AB = \frac{1}{2}AC $, 则点 $ B $ 是线段 $ AC $ 的中点
答案:B
2. (2025·长春期末)已知点 $ P $ 在线段 $ AB $ 上,则下列条件中,不能确定点 $ P $ 是线段 $ AB $ 的中点的是 (
C
)
A.$ AB = 2AP $
B.$ BP = \frac{1}{2}AB $
C.$ AP + BP = AB $
D.$ BP = AP $
答案:C
解析:
解:
A. 若 $ AB = 2AP $,且点 $ P $ 在线段 $ AB $ 上,则 $ AP = \frac{1}{2}AB $,点 $ P $ 是中点;
B. 若 $ BP = \frac{1}{2}AB $,且点 $ P $ 在线段 $ AB $ 上,则点 $ P $ 是中点;
C. 若 $ AP + BP = AB $,仅能说明点 $ P $ 在线段 $ AB $ 上,不能确定是中点;
D. 若 $ BP = AP $,且点 $ P $ 在线段 $ AB $ 上,则点 $ P $ 是中点。
答案:C
3. 在线段 $ MN $ 上,分别以点 $ M,N $ 为圆心, $ c $ 为半径画弧,交线段 $ MN $ 于点 $ E,F $,如图所示,则线段 $ MF $ 与 $ NE $ 的大小关系是 (
C
)
A.$ MF > NE $
B.$ MF < NE $
C.$ MF = NE $
D.不能确定
答案:C
解析:
解:
∵以点M为圆心,c为半径画弧交MN于点E,
∴ME = c。
∵以点N为圆心,c为半径画弧交MN于点F,
∴NF = c。
设MN = a,则MF = MN - NF = a - c,
NE = MN - ME = a - c。
∴MF = NE。
答案:C
4. 线段 $ AB = 3cm $, 延长线段 $ AB $ 到点 $ C $, 使 $ BC = 2AB $, 那么 $ AC = $
9
$ cm $.
答案:9
解析:
解:因为 $ AB = 3\ \text{cm} $,$ BC = 2AB $,所以 $ BC = 2 × 3 = 6\ \text{cm} $。
又因为点 $ C $ 在 $ AB $ 的延长线上,所以 $ AC = AB + BC = 3 + 6 = 9\ \text{cm} $。
9
5. 教材P161习题T6变式 (1)(日照中考)如图,已知 $ AB = 8cm $, $ BD = 3cm $, $ C $ 为线段 $ AB $ 的中点,则线段 $ CD $ 的长为______
1
$ cm $.
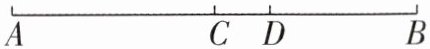
(2)如图, $ C,D $ 是线段 $ AB $ 上两点. 若 $ CB = 4cm $, $ DB = 7cm $, 且 $ D $ 是线段 $ AC $ 的中点,则线段 $ AC $ 的长为______
6
$ cm $.

答案:(1)1 (2)6
解析:
(1)
∵C为线段AB的中点,AB=8cm,
∴BC=AB/2=8/2=4cm。
∵BD=3cm,
∴CD=BC-BD=4-3=1cm。
答案:1
(2)
∵CB=4cm,DB=7cm,
∴DC=DB-CB=7-4=3cm。
∵D是线段AC的中点,
∴AC=2DC=2×3=6cm。
答案:6
6. 用圆规判断三角形各边长度(保留作图痕迹),并在图中“$ ◯ $”

内添上字母 $ A,B,C $,使 $ AC < AB < BC $.
答案:如图所示,$AC < AB < BC$。

7. 如图,已知平面内两点 $ A,B $.
(1) 用尺规按下列要求作图,并保留作图痕迹:
①连接 $ AB $;
②在线段 $ AB $ 的延长线上取点 $ C $,使 $ BC = AB $;
③在线段 $ BA $ 的延长线上取点 $ D $,使 $ AD = AC $.
(2) 写出线段 $ BD $ 与线段 $ AC $ 长度之间的数量关系: $ BD = $
$\frac{3}{2}$
$ AC $;
(3) 若 $ AB = 3cm $, 则 $ AC $ 的长度为
6
$ cm $, $ BD $ 的长度为
9
$ cm $, $ CD $ 的长度为
12
$ cm $.

答案:(1)如图,点D,点C即为所求。

(2)$\frac{3}{2}$ 解析:由作图可知,$AB = BC = \frac{1}{2}AD$,所以$BD = 3BC$,$AC = 2BC$,所以$BD = \frac{3}{2}AC$。
(3)6 9 12
解析:
(1)①以A为起点,B为终点,用直尺连接A、B两点,得到线段AB;②分别以A、B为圆心,以AB长为半径画弧,在线段AB延长线上交于点C;③分别以A、C为圆心,以AC长为半径画弧,在线段BA延长线上交于点D。(作图痕迹保留)
(2)$\frac{3}{2}$
(3)6;9;12
8. 如图,线段 $ AB $ 被点 $ C,D $ 分成 $ 2:4:7 $ 的三部分, $ M,N $ 分别是线段 $ AC,DB $ 的中点,且 $ MN = 17cm $,求线段 $ AB $ 的长.

答案:由线段AB被点C,D分成$2:4:7$的三部分,可设$AC = 2k(k > 0)$,则$CD = 4k$,$BD = 7k$,则$AB = 2k + 4k + 7k = 13k$。因为M,N分别是线段AC,DB的中点,所以$CM = \frac{1}{2}AC = k$,$DN = \frac{1}{2}BD = \frac{7}{2}k$。又因为$MN = 17cm$,$MN = MC + CD + DN$,所以$k + 4k + \frac{7}{2}k = 17$,解得$k = 2$,所以$AB = 13k = 13×2 = 26(cm)$。
解析:
解:设 $ AC = 2k $($ k > 0 $),则 $ CD = 4k $,$ BD = 7k $,
$ AB = AC + CD + BD = 2k + 4k + 7k = 13k $。
因为 $ M $ 是 $ AC $ 的中点,所以 $ CM = \frac{1}{2}AC = k $;
因为 $ N $ 是 $ DB $ 的中点,所以 $ DN = \frac{1}{2}BD = \frac{7}{2}k $。
又因为 $ MN = MC + CD + DN = 17\,\text{cm} $,
所以 $ k + 4k + \frac{7}{2}k = 17 $,
解得 $ k = 2 $。
因此,$ AB = 13k = 13 × 2 = 26\,\text{cm} $。
答:线段 $ AB $ 的长为 $ 26\,\text{cm} $。
9. 如图,点 $ A,B,C $ 顺次在直线 $ l $ 上,点 $ M $ 是线段 $ AC $ 的中点,点 $ N $ 是线段 $ BC $ 的中点,若想求出 $ MN $ 的长度,那么只需条件 (
A
)
A.$ AB = 16 $
B.$ BC = 3 $
C.$ AM = 4 $
D.$ CN = 1 $
答案:A 解析:因为$MN = BM + BN = MC - NC = \frac{1}{2}AC - \frac{1}{2}BC = \frac{1}{2}(AC - BC) = \frac{1}{2}AB$,故选A。