10.教材P142练习T2变式 如图,左边的几何体叫三棱柱,它有5个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
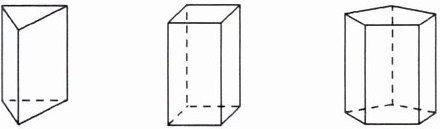
(1)四棱柱有
8
个顶点,
12
条棱,
6
个面.
(2)五棱柱有
10
个顶点,
15
条棱,
7
个面.
(3)你能由此猜出六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
六棱柱有12个顶点，18条棱，8个面；七棱柱有14个顶点，21条棱，9个面。
(4)n棱柱有几个顶点,几条棱,几个面?
n棱柱有2n个顶点，3n条棱，(n+2)个面。
答案：【解析】：本题主要考查对棱柱性质的理解和应用。
(1) 对于四棱柱，可以从给出的四棱柱图形中直接观察到其顶点数、棱数和面数。
(2) 对于五棱柱，同样可以从给出的五棱柱图形中直接观察到其顶点数、棱数和面数。
(3) 对于六棱柱和七棱柱，需要根据前面的观察结果进行推理。
(4) 对于n棱柱，需要找出顶点数、棱数和面数与棱数n之间的关系。
【答案】：
(1) 四棱柱有8个顶点，12条棱，6个面。
(2) 五棱柱有10个顶点，15条棱，7个面。
(3) 六棱柱有12个顶点，18条棱，8个面；七棱柱有14个顶点，21条棱，9个面。
(4) n棱柱有2n个顶点，3n条棱，(n+2)个面。
11.探究:如图,将一个正方体表面全部涂上颜色.
(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,我们把仅有i个面涂色的小正方体的个数记为$x_{i}$,那么$x_{3}= $
8
,$x_{2}= $
12
,$x_{1}= $
6
,$x_{0}= $
1
;
(2)如果把正方体的棱四等分,同样沿等分线把正方体切开,得到64个小正方体,那么$x_{3}= $
8
,$x_{2}= $
24
,$x_{1}= $
24
,$x_{0}= $
8
;
(3)如果将这个正方体的棱n等分(n大于3),沿等分线把正方体切开,得到$n^{3}$个小正方体,且满足$2x_{2}-x_{3}= 208$,求n的值.
由 (1)(2) 可得 $x_3 = 8$，$x_2 = 12(n - 2)$，代入 $2x_2 - x_3 = 208$，即 $2×12(n - 2) - 8 = 208$，解得 $n = 11$.
答案：(1) 8 12 6 1 解析：由题图可知，3 个面涂色的小正方体在原正方体的顶点处，共有 8 个，故 $x_3 = 8$；2 个面涂色的小正方体在每条棱的中间处，共有 12 个，故 $x_2 = 12$；1 个面涂色的小正方体在原正方体每个面的中心处，共有 6 个，故 $x_1 = 6$；没有涂色的小正方体在原正方体的中心处，有 1 个，故 $x_0 = 1$，故答案为 8，12，6，1.；(2) 8 24 24 8；(3) 由 (1)(2) 可得 $x_3 = 8$，$x_2 = 12(n - 2)$，代入 $2x_2 - x_3 = 208$，即 $2×12(n - 2) - 8 = 208$，解得 $n = 11$.
解析：
(1) 8；12；6；1
(2) 8；24；24；8
(3) 解：由题意得，$x_{3}=8$，$x_{2}=12(n-2)$
∵$2x_{2}-x_{3}=208$
∴$2×12(n-2)-8=208$
$24(n-2)=216$
$n-2=9$
$n=11$
12.若将棱长为2的正方体切成8个棱长为1的小正方体,则所有小正方体表面积的和是原正方体表面积的
2
倍;若将棱长为3的正方体切成27个棱长为1的小正方体,则所有小正方体表面积的和是原正方体表面积的
3
倍;若将棱长为$n(n＞1$,n为整数)的正方体切成$n^{3}$个棱长为1的小正方体,则所有小正方体表面积的和是原正方体表面积的
n
倍.
答案：2 3 $n$ 解析：棱长为 $n(n ＞ 1$，$n$ 为整数) 的正方体的表面积是 $6n^2$，把它切成 $n^3$ 个棱长为 1 的小正方体，则每个小正方体的表面积是 6，则所有小正方体表面积的和是 $6n^3$，所以所有小正方体表面积的和是原正方体表面积的 $n$ 倍.
解析：
解：棱长为2的正方体表面积为$6×2^2=24$，切成8个棱长为1的小正方体，每个小正方体表面积为$6×1^2=6$，所有小正方体表面积和为$8×6=48$，$48÷24=2$；
棱长为3的正方体表面积为$6×3^2=54$，切成27个棱长为1的小正方体，所有小正方体表面积和为$27×6=162$，$162÷54=3$；
棱长为$n$的正方体表面积为$6n^2$，切成$n^3$个棱长为1的小正方体，所有小正方体表面积和为$n^3×6=6n^3$，$6n^3÷6n^2=n$。
2；3；$n$
13.十八世纪瑞士数学家欧拉发现了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据图中的多面体模型,完成表格:
|多面体|顶点数(V)|面数(F)|棱数(E)|
|四面体|4|4|
6
|
|长方体|8|6|12|
|正八面体|
6
|8|12|
|正十二面体|20|12|30|
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是:
E = V + F - 2
.
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是
20
.
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,每个顶点处都有3条棱,且每个顶点都是3个面的交点,已知共有棱36条.求该多面体外表面三角形的个数.
因为 $E = 36 = \frac{3V}{2}$，所以 $V = 24$。又因为 $V + F - E = 2$，所以 $F = 14$。设三角形的个数为 $x$，则八边形的个数为 $14 - x$，每个三角形有 3 个顶点，每个八边形有 8 个顶点，且因为每个顶点都是 3 个面的交点，共有 24 个顶点，所以 $\frac{3x + 8(14 - x)}{3} = 24$，解得 $x = 8$，所以该多面体外面三角形的个数为 8。
答案：(1) 6 6 $E = V + F - 2$；(2) 20 解析：由题意得 $F - 8 + F - 30 = 2$，解得 $F = 20$. 故答案为 20.；(3) 因为 $E = 36 = \frac{3V}{2}$，所以 $V = 24$. 又因为 $V + F - E = 2$，所以 $F = 14$. 设三角形的个数为 $x$，则八边形的个数为 $14 - x$，每个三角形有 3 个顶点，每个八边形有 8 个顶点，且因为每个顶点都是 3 个面的交点，共有 24 个顶点，所以 $\frac{3x + 8(14 - x)}{3} = 24$，解得 $x = 8$，所以该多面体外面三角形的个数为 8.
解析：
(1) 6；6；$V+F-E=2$
(2) 20
(3) 解：因为$E=36=\frac{3V}{2}$，所以$V=24$。
由$V+F-E=2$，得$F=E-V+2=36-24+2=14$。
设三角形的个数为$x$，则八边形的个数为$14-x$。
由题意得$\frac{3x+8(14-x)}{3}=24$，解得$x=8$。
答：该多面体外表面三角形的个数为8。
