13. 教材P21习题T5变式 如图,在数轴上有三个点A,B,C,请回答下列问题:
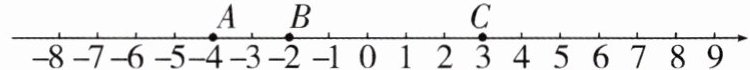
(1)将点B向左移动3个单位长度后,三个点所表示的数中谁最小? 是多少?
(2)将点A向右移动4个单位长度后,三个点所表示的数中谁最小? 是多少?
(3)若每个点只能移动一次,怎样移动A,B,C中的两点,才能使三个点表示的数相同?有几种移动方法?
答案:(1)将点B向左移动3个单位长度后,三个点所表示的数中点B表示的数最小,是−5.
(2)将点A向右移动4个单位长度后,三个点所表示的数中点B表示的数最小,是−2.
(3)把点A向右移动7个单位长度,点B向右移动5个单位长度,这时A,B,C三点都表示3;把点A向右移动2个单位长度,点C向左移动5个单位长度,这时A,B,C三点都表示−2;把点B向左移动2个单位长度,点C向左移动7个单位长度,这时A,B,C三点都表示−4.共有3种移动方法.
14. 新考法 如图①,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上表示1与2这两个数的点空心,表示这个范围不包含数1和2).如图②,这个“范围”包含所有不小于-1且不大于3的数(数轴上表示-1与3这两个数的点实心,表示这个范围包含数-1和3).
请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于-3且小于0的数(画在图③上).
(2)包含-1.5,π这两个数,且只含有5个整数(画在图④上).
(3)同时满足以下两个条件:(画在图⑤上)
①有最小的正整数;
②这个范围内最大的数与最小的数表示的点的距离大于3但小于4.

答案:(1)画图如下:
。:。−2−1−3
(2)答案不唯一,画图如下:

(3)答案不唯一,画图如下:

15. 新题型 新定义 (2025·台州期末)一般用[x]表示不大于x的最大整数,如[1.8]= 1.现规定$\{x\}= x-[x]$,如$\{2\}= 2-[2]= 2-2= 0$;$\{-3.1\}= (-3.1)-[-3.1]= (-3.1)-(-4)= 0.9$.可借助数轴上两点之间的距离理解$\{x\}$的意义,如图,表示2与[2]的点A,B重合,所以$\{2\}= 0$;表示-3.1与[-3.1]的点C,D距离为0.9,所以$\{-3.1\}= CD= 0.9$.
(1)分别求$\{1.8\}$与$\{-1.8\}$的值;
(2)当a > 0时,
①$\{a\}+\{-a\}$的值为
0或1
;
②已知$\{-a\}= 0.4$,求$\{a+1\}+\{a+2\}+…+\{a+10\}$的值;
(3)当a > 0时,$\{4a\}= \{a\}$,请直接写出$\{a\}$的值.
(1)解:$\{1.8\}=1.8 - [1.8]=1.8 - 1=0.8$,$\{-1.8\}=(-1.8)-[-1.8]=(-1.8)-(-2)=0.2$。
(2)②解:因为$\{-a\}=0.4$,所以$\{a\}=1 - \{-a\}=1 - 0.4=0.6$,$\{a + 1\}=\{a + 2\}=...=\{a + 10\}=\{a\}$,所以$\{a + 1\}+\{a + 2\}+…+\{a + 10\}=0.6×10=6$。
(3)
0或$\frac{1}{3}$或$\frac{2}{3}$
答案:(1)|1.8|=1.8 - [1.8]=1.8 - 1=0.8,|-1.8|=(-1.8)-[-1.8]=(-1.8)-(-2)=0.2.
(2)①0或1 解析:因为a>0,所以当a为整数时,[a]=a,[-a]= - a,所以|a|=a - [a]=0,|-a|= - a - [-a]=0,所以|a|+|-a|=0;当a不是整数时,由题意得|a|等于a的小数部分,|-a|等于a的整数部分加1后再减去a,所以|a|+|-a|=1.
②因为|-a|=0.4,所以|a|=1 - |-a|=1 - 0.4=0.6,|a + 1|=|a + 2|=...=|a + 10|=|a|,所以|a + 1|+|a + 2|+…+|a + 10|=0.6×10=6.
(3)|a|=0或$\frac{1}{3}$或$\frac{2}{3}$ 解析:因为a>0时,|4a|=|a|,所以4a与a的小数部分相同,所以a的小数部分只能是0或使得4倍后小数部分不变的值,即a的小数部分为0或$\frac{1}{3}$或$\frac{2}{3}$,所以|a|=0或$\frac{1}{3}$或$\frac{2}{3}$.