1. (2024·东营中考改编)-3的绝对值是(
A
)
A.3
B.-3
C.±3
D.0
答案:A
解析:
解:根据绝对值的定义,负数的绝对值是它的相反数。-3是负数,所以-3的绝对值是3。
答案:A
2. (广州中考)a,b在数轴上的位置如图所示,则(
C
)
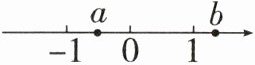
A.a = b
B.a > b
C.|a| < |b|
D.|a| > |b|
答案:C
解析:
由数轴可知:$-1 < a < 0$,$1 < b$。
$|a|$表示$a$到原点的距离,$|b|$表示$b$到原点的距离。
因为$a$到原点的距离小于$1$,$b$到原点的距离大于$1$,所以$|a| < |b|$。
C
3. 下列说法正确的是(
D
)
A.任何数的绝对值都是正数
B.若a,b都是有理数,且a > b,那么|a| > |b|
C.如果|a| > |b|,那么a > b
D.绝对值等于它本身的是非负数
答案:D
解析:
解:
A. 0的绝对值是0,不是正数,故A错误;
B. 若a=1,b=-2,a>b,但|a|=1<|b|=2,故B错误;
C. 若|a|=3,|b|=2,当a=-3时,a<b,故C错误;
D. 绝对值等于它本身的数是非负数,故D正确。
答案:D
4. 计算:
(1) |-9| - |$- \frac{4}{9}$| - |$- \frac{5}{9}$| =
8
;
(2) |$- \frac{8}{3}$| × |$- \frac{5}{8}$| ÷ |$- \frac{1}{12}$| =
20
.
答案:(1)8 (2)20
解析:
(1)解:原式=9 - $\frac{4}{9}$ - $\frac{5}{9}$
=9 - ($\frac{4}{9}$ + $\frac{5}{9}$)
=9 - 1
=8
(2)解:原式=$\frac{8}{3}$ × $\frac{5}{8}$ ÷ $\frac{1}{12}$
=$\frac{5}{3}$ × 12
=20
5. (1)(镇江中考)已知一个数的绝对值是4,则这个数是
±4
.
(2)新趋势 开放性试题(2025·济宁期末)已知整数m同时满足下列两个条件:①在数轴上位于原点左侧;②绝对值大于2且小于6.写出一个符合条件的m的值:
-3
.
答案:(1)$\pm 4$ (2)-3(答案不唯一)
6. 教材P24练习T1变式用数轴上的点表示下列各数,并写出这些数的绝对值$.-1 \frac{1}{2}, 2, 3, -2, 1 \frac{1}{2}, -3, 0.$
答案:如图所示

$\left|-1\frac{1}{2}\right|=1\frac{1}{2},|2|=2,|3|=3,|-2|=2,\left|1\frac{1}{2}\right|=1\frac{1}{2},|-3|=3,|0|=0$.
7. 按要求写出下列各数:
(1)写出所有绝对值不大于4的整数;
(2)写出所有绝对值大于1且小于4的整数.
答案:(1)要求绝对值不大于4的整数,即求数轴上到原点的距离不大于4的整数点,如图所示
-5-4-3-2-10123456
所以符合要求的数有-4,-3,-2,-1,0,1,2,3,4.
(2)与(1)类似,在数轴上找出相应的整数点,如图所示.
-5-4-3-2-1012345
所以符合要求的数有-3,-2,2,3.
8. (2025·郑州期末)如图,数轴的单位长度为1,如果点B,C表示的数的绝对值相等,那么点A表示的数是( )

A.-2
B.-4
C.-5
D.-6
答案:B 解析:如图,由点B,C表示的数的绝对值相等,得原点O的位置,且数轴的单位长度为1,所以点A表示的数是-4,故选B.

9. 给出下列结论:①若|m| > 0,则m > 0;②若m > n,则|m| > |n|;③若|m| > |n|,则m > n;④对于任意数m,|m|是正数;⑤在数轴上,离原点越远,该点对应的数的绝对值越大.其中正确结论的个数为(
B
)
A.0
B.1
C.2
D.3
答案:B 解析:①若$|m|>0$,则$m<0$或$m>0$,故①错误;②由$1>-2,|1|<|-2|$,故②错误;③由$|-2|>|1|,-2<1$,故③错误;④对于任意数m,$|m|$是正数或0,故④错误;⑤在数轴上,离原点越远,该点对应的数的绝对值越大,故⑤正确。综上,正确结论的个数为1,故选B.
10. 检查5个篮球的质量,把超过标准质量的克数记作正数,不足的克数记作负数,检查结果如表:
| 篮球的编号 | 1 | 2 | 3 | 4 | 5 |
| 与标准质量的差/g | +4 | +7 | -3 | -8 | +9 |
(1)最接近标准质量的是
3
号篮球;
(2)质量最大的篮球比质量最小的篮球重
17
g.
答案:(1)3 (2)17