8. (1)如图①,小明将一张正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为
80
$cm^{2}$.
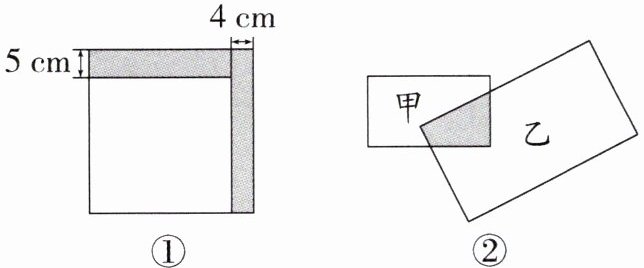
(2)新考法(2024·泰州月考)如图②,甲、乙两个长方形有一部分重叠在一起,甲长方形不重叠的部分是甲长方形面积的$\frac {2}{3}$,乙长方形不重叠的部分是乙长方形面积的$\frac {5}{7}$,且甲、乙两个长方形面积之和为$52cm^{2}$,则重叠部分面积是
8
$cm^{2}$.
答案:(1) $ 80 $ 解析:设原来正方形纸片的边长是 $ x \, \text{cm} $,则第一次剪下的长条的长是 $ x \, \text{cm} $,宽是 $ 4 \, \text{cm} $,第二次剪下的长条的长是 $ (x - 4) \, \text{cm} $,宽是 $ 5 \, \text{cm} $,则 $ 4x = 5(x - 4) $,解得 $ x = 20 $,$ 20×4 = 80(\text{cm}^2) $。故每一个长条的面积为 $ 80 \, \text{cm}^2 $。
(2) $ 8 $ 解析:设甲长方形的面积为 $ x \, \text{cm}^2 $,则乙长方形的面积为 $ (52 - x) \, \text{cm}^2 $,由题意,得 $ \left(1 - \frac{2}{3}\right)x = \left(1 - \frac{5}{7}\right)(52 - x) $,解得 $ x = 24 $,所以重叠部分面积是 $ \left(1 - \frac{2}{3}\right)x = \frac{1}{3}×24 = 8(\text{cm}^2) $。
9. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图①,小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图②那样的正方形,中间还留下了一个洞,恰好是面积为$9cm^{2}$的小正方形,求每个小长方形的面积.

答案:由题图②得中间小正方形的边长为 $ 3 \, \text{cm} $,设每个小长方形的宽为 $ y \, \text{cm} $,由题图②可知每个小长方形的长为 $ (2y - 3) \, \text{cm} $,根据题图①列方程 $ 3(2y - 3) - 5y = 0 $,解得 $ y = 9 $,所以 $ 2y - 3 = 15(\text{cm}) $,所以每个小长方形的面积为 $ 9×15 = 135(\text{cm}^2) $。
答:每个小长方形的面积为 $ 135 \, \text{cm}^2 $。
10. 新考法(2025·南宁期中)对联是中华传统文化的瑰宝.如图①所示,对联装裱后,上、下空白处分别称为天头和地头,左、右空白处统称为边.一般情况下,天头长与地头长的比是6:4,左、右边的边宽相等,且为天头长与地头长的和的$\frac {1}{10}$,设左、右边的边宽为xcm.
(1)用含x的代数式分别表示天头长和地头长.
(2)现要装裱一副五言联,该五言联的长为92cm,宽为25cm,如图②所示,装裱五言联用的卷轴的长是宽的4倍.求五言联装裱预留的天头长.
(3)如图③,徐老师裁出两张长方形纸张准备写一副七言联,每张正好划出7个正方形方格,正方形方格的边长为acm.若装裱用的卷轴长为190cm,正方形方格的边长比装裱后的边宽大,且两者长度均为整数,求徐老师裁剪的长方形纸张的长.

答案:(1) 因为左、右边的边宽为 $ x \, \text{cm} $,且为天头长与地头长的和的 $ \frac{1}{10} $,所以天头长与地头长的和为 $ 10x \, \text{cm} $。因为天头长与地头长的比是 $ 6:4 $,所以天头长为 $ 10x·\frac{6}{6 + 4} = 6x \, \text{cm} $,地头长为 $ 10x·\frac{4}{6 + 4} = 4x \, \text{cm} $。
(2) 根据题意,装裱五言联用的卷轴的长为 $ (92 + 10x) \, \text{cm} $,宽为 $ (25 + 2x) \, \text{cm} $。
因为卷轴的长是宽的 $ 4 $ 倍,所以 $ 92 + 10x = 4(25 + 2x) $,解得 $ x = 4 $,所以 $ 6x = 6×4 = 24(\text{cm}) $,所以五言联装裱预留的天头长 $ 24 \, \text{cm} $。
(3) 因为装裱用的卷轴长为 $ 190 \, \text{cm} $,所以 $ 7a + 10x = 190 $,所以 $ a = \frac{190 - 10x}{7} $。因为 $ a > x $,$ a $ 与 $ x $ 都是正整数,所以 $ x = 5 $,$ a = 20 $,所以 $ 7a = 7×20 = 140(\text{cm}) $,所以徐老师裁剪的长方形纸张的长为 $ 140 \, \text{cm} $。