1. (2024·衢州期末)如图,一雕塑的底面呈正方形,在其左右侧及后方种植宽度均为3m的草坪.若草坪总面积为$90m^{2}$,设雕塑的底面边长为xm,则有 (
B
)
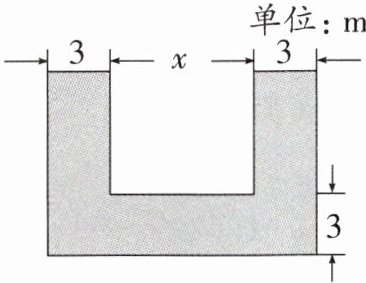
A.$2×3x+3(x+3)= 90$
B.$2×3(x+3)+3x= 90$
C.$3×3(x+3)= 90$
D.$3×\frac {3(x+x+3)}{2}= 90$
答案:B
2. 一个底面半径为10cm、高为20cm的圆柱形大杯中装满了水,把水倒入底面半径为5cm的圆柱形小杯中,刚好倒满8杯,则小杯的高为
10
cm.
答案:10
解析:
解:设小杯的高为$h$cm。
圆柱体积公式$V = \pi r^2 h$。
大杯体积:$\pi × 10^2 × 20 = 2000\pi$($cm^3$)
8个小杯体积:$8 × \pi × 5^2 × h = 200\pi h$($cm^3$)
由题意得$200\pi h = 2000\pi$
解得$h = 10$
10
3. 教材P126练习T3变式(2025·贵阳期末)将一根绳子折成4段,按如图①所示方式,剪一刀,绳子变为5段;如图②,剪两刀,绳子变为9段;如图③,…,按照这样的规律,若想要剪得2025段绳子,则需要剪
506
刀.

答案:506
解析:
解:设剪$n$刀,绳子段数为$y$。
由题意:
剪1刀,$y=5=4×1 + 1$;
剪2刀,$y=9=4×2 + 1$;
剪3刀,$y=13=4×3 + 1$;
规律:$y=4n + 1$。
令$4n + 1=2025$,
解得$n=506$。
答案:506
4. 新趋势 数学文化 元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”
答案:设原来有 $ x $ 斗酒,根据题意,得 $ 2[2(x + x - 1) - 1] - 1 = 0 $,解得 $ x = 0.875 $。答:原来有 $ 0.875 $ 斗酒。
5. (2024·北京模拟)在房山区践行“原色育人,生态发展”教育发展理念的引领下,某校为提升实践育人实效,积极组织学生建设劳动基地,参与校园种植活动.计划在校园内一块长方形的空地上开垦两块完全相同的长方形菜园,如图所示,已知空地长10m,宽4.5m,长方形菜园的长与宽的比为6:1,并且预留的上、中、下、左、右通道的宽度相等,那么预留通道的宽度和长方形菜园的宽分别是多少米?

答案:设长方形菜园的宽为 $ x \, \text{m} $,则长为 $ 6x \, \text{m} $,根据题意,得 $ \frac{1}{2}(10 - 6x) = \frac{1}{3}(4.5 - 2x) $,解得 $ x = 1.5 $。
所以预留通道的宽度 $ = \frac{1}{3}(4.5 - 2x) = 0.5(\text{m}) $。
答:预留通道的宽度是 $ 0.5 \, \text{m} $,长方形菜园的宽是 $ 1.5 \, \text{m} $。
6. 如图,将图①正方形作如下操作:第1次:分别连接各边中点如图②,得到5个正方形;第2次:将图②左上角正方形按上述方法再分割如图③,得到9个正方形……以此类推,根据以上操作,正方形的个数不可能为 (
C
)
A.2021
B.2025
C.2027
D.2029
答案:C 解析:题图①有 $ 1 $ 个正方形,题图②有 $ 1 + 4×(2 - 1) = 5 $(个)正方形,题图③有 $ 1 + 4×(3 - 1) = 9 $(个)正方形……以此类推,图 $ \overline{n} $ 有 $ 1 + 4(n - 1) = (4n - 3) $ 个正方形。当正方形的个数是 $ 2021 $ 时,解得 $ n = 506 $,当正方形的个数是 $ 2025 $ 时,解得 $ n = 507 $,当正方形的个数是 $ 2027 $ 时,解得 $ n = 507.5 $,当正方形的个数是 $ 2029 $ 时,解得 $ n = 508 $,因为 $ n $ 是正整数,所以正方形的个数不可能为 $ 2027 $。故选 C。
7. (2025·成都期中)有一玻璃密封器皿如图①,测得其底面直径为20cm,高20cm,现内装溶液若干.如图②放置时,测得液面高10cm,如图③放置时,测得液面高16cm,则该玻璃密封器皿总容量为(结果保留π) (
D
)
A.$1250πcm^{3}$
B.$1300πcm^{3}$
C.$1350πcm^{3}$
D.$1400πcm^{3}$
答案:D 解析:设该玻璃密封器皿总容量为 $ V \, \text{cm}^3 $,根据题意,得 $ \pi×10^2×10 = V - \pi×10^2×(20 - 16) $,解得 $ V = 1400\pi $。故选 D。