例1（教材P70）
西塘小学六年级同学要植一些树（不超过100棵）。如果每行植6棵，最后一行缺1棵；如果每行植5棵或4棵，最后一行也都缺1棵。这批树苗有多少棵？
答案：4、5、6的最小公倍数是60。
60-1=59（棵）
59＜100，符合题意。
答：这批树苗有59棵。
1. 某合唱队有若干人，如果每12人站一排，那么余5人；如果每15人站一排，那么还是余5人。这个合唱队至少有多少人？
答案：1. 12和15的最小公倍数是60。
60+5=65（人）
这个合唱队至少有65人。
[提示]先求出12和15的最小公倍数，再加上5人，就是这个合唱队至少有的人数。
例2（教材P80）
有两支蜡烛，当第一支燃去$\frac{4}{5}$，第二支燃去$\frac{2}{3}$时，剩下的部分一样长。这两支蜡烛原来长度的比是几比几？
答案：$1-\frac{4}{5}=\frac{1}{5}$
$1-\frac{2}{3}=\frac{1}{3}$
$\frac{1}{3}:\frac{1}{5}=5:3$
答：这两支蜡烛原来长度的比是$5:3$。
2. 有两支蜡烛，当第一支燃去$\frac{1}{3}$，第二支燃去$\frac{1}{4}$时，剩下的部分一样长。这两支蜡烛原来长度的比是几比几？
答案：2. 1-$\frac{1}{3}$=$\frac{2}{3}$ 1-$\frac{1}{4}$=$\frac{3}{4}$
$\frac{3}{4}$：$\frac{2}{3}$=9：8
[提示]第一支蜡烛剩下部分的长度是蜡烛原来长度的1-$\frac{1}{3}$=$\frac{2}{3}$，第二支蜡烛剩下部分的长度是蜡烛原来长度的1-$\frac{1}{4}$=$\frac{3}{4}$，两支蜡烛剩下的部分一样长，因此第一支蜡烛原来长度×$\frac{2}{3}$=第二支蜡烛原来长度×$\frac{3}{4}$，根据比例的基本性质可知，第一支蜡烛原来长度：第二支蜡烛原来长度=$\frac{3}{4}$：$\frac{2}{3}$=9：8。
例3（教材P88）
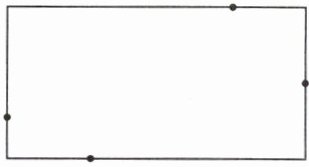
右图是一个长方形框架，上面有4枚钉子。在每两枚钉子间拉上一条线后，框架内共有多少个三角形？你知道它们各是什么三角形吗？
答案：思路分析按要求画图解答。在任意两点间画一条线段，如下图：
解答：框架内共有12个三角形。其中有2个锐角三角形、6个钝角三角形和4个直角三角形。归纳点拨三角形的三个顶点不能在一条直线上，在数三角形个数时做到不重复、不遗漏。
