一、填一填。(每空 1 分,共 22 分)
1. (
15
):20 = $\frac{(\ )}{24}$ = 12÷(
16
) = 0.75 = (
75
)%
答案:1. 15 18 16 75 [提示]连等式表示各部分都等于0.75,( ):20=0.75,括号内为0.75×20=15;$\frac{( )}{24}$=0.75,括号内为0.75×24=18;12÷( )=0.75,括号内为12÷0.75=16;0.75=75%。
2. 电脑上有一张长 5 厘米、宽 1.8 厘米的图片,拖动鼠标将图片放大后,图片的长变成了 20 厘米,相当于把这张图片按(
4:1
)的比放大了,则图片的宽变成了(
7.2
)厘米。
答案:2. 4:1 7.2 [提示]20:5=4:1,即图片按4:1的比放大,放大后图片的宽为1.8×4=7.2(厘米)。
3. 一个圆柱形钢锭的底面直径是 10 厘米,高是 6 厘米,它的侧面积是(
188.4
)平方厘米,表面积是(
345.4
)平方厘米,体积是(
471
)立方厘米。把它熔铸成一个与圆柱底面积和体积相等的圆锥,圆锥的高是(
18
)厘米。
答案:3. 188.4 345.4 471 18 [提示]根据圆柱的侧面积公式$S = π dh$计算出圆柱的侧面积;用直径除以2计算出底面半径,根据圆的面积公式$S = π r^{2}$计算出圆柱的底面积,底面积乘2加上侧面积即可计算出圆柱的表面积;根据圆柱的体积公式$V = π r^{2}h$计算出圆柱的体积。把它熔铸成一个与圆柱底面积和体积相等的圆锥,圆锥的高是圆柱高的3倍。
解析:
侧面积:$S_{侧}=πdh=3.14×10×6=188.4$(平方厘米)
底面积:$r = 10÷2 = 5$(厘米),$S_{底}=πr^{2}=3.14×5^{2}=78.5$(平方厘米)
表面积:$S_{表}=2S_{底}+S_{侧}=2×78.5 + 188.4 = 157 + 188.4 = 345.4$(平方厘米)
体积:$V = S_{底}h = 78.5×6 = 471$(立方厘米)
圆锥的高:因为圆锥体积$V=\frac{1}{3}S_{底}h_{锥}$,且$V$、$S_{底}$与圆柱相等,所以$h_{锥}=3h = 3×6 = 18$(厘米)
188.4;345.4;471;18
4. 学校围棋社团的男生人数比女生人数多 18 人,男生人数占总人数的$\frac{5}{8}$,男生有(
45
)人,女生有(
27
)人。
答案:4. 45 27 [提示]女生人数占总人数的$1 - \frac{5}{8} = \frac{3}{8}$,男生人数比女生人数多占总人数的$\frac{5}{8} - \frac{3}{8} = \frac{1}{4}$,总人数为$18 ÷ \frac{1}{4} = 72$(人),那么男生有$72 × \frac{5}{8} = 45$(人),女生有45 - 18 = 27(人)。
5. 在一幅地图上,量得南京到上海的距离是 15 厘米,南京到上海的实际距离约是 300 千米,这幅地图的比例尺是(
1:2000000
);图上 1 厘米表示的实际距离是(
20
)千米;南京到淮安的实际距离约是 200 千米,在这幅地图上,南京到淮安的图上距离是(
10
)厘米。
答案:5. 1:2000000 20 10 [提示]根据“比例尺=图上距离:实际距离”计算出比例尺为1:2000000;由比例尺1:2000000可知,图上距离1厘米表示实际距离2000000厘米,即20千米;已知南京到淮安的实际距离约是200千米,用200除以20即可计算出南京到淮安的图上距离。
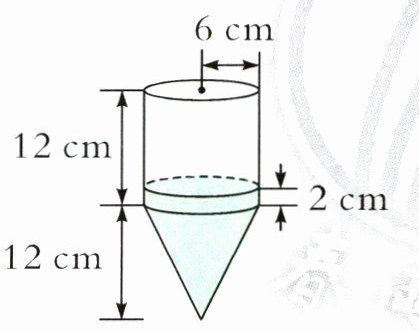
6. 底面半径和高分别是 6 厘米、12 厘米的空心圆锥和空心圆柱各一个,组成竖放的容器(如图)。在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高 2 厘米。若将这个容器上面封住并倒立,则细沙的高度是(
6
)厘米。
答案:6. 6 [提示]根据“等体积等底面积的圆柱和圆锥中,圆锥的高是圆柱高的3倍”,圆锥部分细沙的高÷3=倒入圆柱部分细沙的高,再加上圆柱部分原来的高,即$12 ÷ 3 + 2 = 6$(厘米)。
解析:
圆锥体积:$\frac{1}{3}πr^{2}h=\frac{1}{3}π×6^{2}×12=144π$(立方厘米)
圆柱部分细沙体积:$πr^{2}h=π×6^{2}×2=72π$(立方厘米)
总细沙体积:$144π + 72π=216π$(立方厘米)
倒立后细沙高度:$h=\frac{V}{πr^{2}}=\frac{216π}{π×6^{2}}=6$(厘米)
6
7. 在一个比例中,两个内项的积是 5,一个外项是 2,另一个外项是(
2.5
)。其中一个内项是 10,这个比例可能是(
2:10=0.5:2.5(比例的写法不唯一)
)。
答案:7. 2.5 2:10=0.5:2.5(比例的写法不唯一) [提示]5÷2=2.5,5÷10=0.5,所以另一个外项是2.5.其中一个内项是10,这个比例可能是2:10=0.5:2.5。
解析:
2.5;2:10=0.5:2.5(比例的写法不唯一)
8. 如果 3×A = B÷2(A、B 均不为 0),那么 A:B = (
1
):(
6
)。
答案:8. 1 6 [提示]由$3 × A = B ÷ 2$,得6A = B,即A:B = 1:6。
解析:
由$3× A = B÷2$,得$3A=\frac{B}{2}$,两边同乘2,$6A = B$,所以$A:B = 1:6$。
9. 把一根 2 米长的圆柱形木料截成 3 段同样的小圆柱,表面积增加了 304 平方厘米,这根木料的体积是(
15200
)立方厘米。
答案:9. 15200 [提示]表面积增加了304平方厘米,即4个底面积之和是304平方厘米,故底面积为304÷4=76(平方厘米),木料长为2米(即200厘米),圆柱体积等于底面积乘高,故这根木料的体积是76×200=15200(立方厘米)。
解析:
2米=200厘米
截成3段,表面积增加4个底面积,底面积为 $304÷4 = 76$ 平方厘米
体积为 $76×200 = 15200$ 立方厘米
15200
10. 鸡兔同笼不知数,三十六头笼中露,数清脚共 100 只。鸡有(
22
)只。
答案:10. 22 [提示]假设都是兔,鸡有$(36 × 4 - 100) ÷ (4 - 2) = 22$(只)。
解析:
假设都是兔,鸡有$(36×4 - 100)÷(4 - 2)=(144 - 100)÷2=44÷2=22$(只)。
1. 下表是六年级学生体育检测成绩情况统计表,扇形统计图(
D
)能准确反映出表中数据。


答案:1. D [提示]先计算各部分人数占总人数的百分比,再根据百分比选择扇形统计图。