9. (生活应用)如图,用混凝土浇筑一个无盖长方体水槽(有底),混凝土厚 1 dm。
(1) 这个水槽的容积是多少?
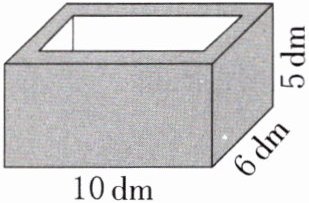
(2) 浇筑这个水槽需要多少立方分米的混凝土?
答案:9. (1)(10 - 1×2)×(6 - 1×2)×(5 - 1)=128(dm³)
128dm³=128L
(2)10×6×5 - 128=172(dm³)
10. (操作探究)有一块长 30 厘米、宽 16 厘米的纸皮,要用它做成一个无盖纸盒。两名同学的方法如下:

(1) 请在图中用虚线表示两名同学的方法。

(2) 请用计算说明哪名同学做的纸盒容积大。(纸皮损耗忽略不计)
答案:10. (1)

(2)小兰:(30 - 4×2)×(16 - 4×2)×4=704(立方厘米)
小丽:(30 - 4)×(16 - 4×2)×4=832(立方厘米)
832>704 小丽做的纸盒容积大
11. 一个长方体被截成两个完全相同的正方体(如图)。两个正方体的棱长之和比原来长方体的棱长之和增加了 16 厘米。原来长方体的表面积是(
40
)平方厘米。
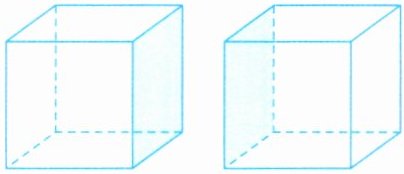
思路提示:长方体被截后,增加了几个正方体
的面?
一共增加了多少条棱?
答案:11. 40 解析:把一个长方体截成两个完全一样的正方体,增加了4×2=8(条)正方体的棱。因为两个正方体的棱长之和比原来长方体的棱长之和增加了16厘米,所以正方体的棱长为16÷8=2(厘米)。因为正方体的棱长是原来长方体长的一半,所以原来长方体的长为2×2=4(厘米)。再根据长方体的表面积公式求解。
解析:
把一个长方体截成两个完全一样的正方体,增加了$4×2 = 8$条正方体的棱。
因为两个正方体的棱长之和比原来长方体的棱长之和增加了16厘米,所以正方体的棱长为$16÷8 = 2$厘米。
原来长方体的长为$2×2 = 4$厘米,宽和高均为2厘米。
长方体表面积为$2×(4×2 + 4×2 + 2×2)$
$=2×(8 + 8 + 4)$
$=2×20$
$=40$平方厘米。
40
12. (思维过程)一个正方体容器从里面量,棱长为 6 分米,里面装有 2 分米深的水。将一个棱长为 4 分米的正方体铁块放入水中,水深变为多少分米?
思路提示:解决物体部分浸入水中的问题时,可运用公式:水的深度=水的体积÷水的底面积。
答案:12. (4×4×4+6×6×2)÷(6×6)=$\frac{34}{9}$(分米) $\frac{34}{9}$<4 铁块没有完全浸入水中
6×6×2÷(6×6 - 4×4)=3.6(分米)
解析:先判断铁块是否完全浸入水中,用“(铁块的体积 + 水的体积)÷容器的底面积”得出假设铁块完全浸入水中时的水深,再与铁块的高度进行比较。如果水深大于或等于铁块的高度,那么铁块完全浸入水中,此时水的深度即为所求;如果水深小于铁块的高度,那么铁块没有完全浸入水中,此时水的体积不变,容器中水的底面积=容器的底面积 - 铁块的底面积,则水深=水的体积÷(容器的底面积 - 铁块的底面积)。
13. 有两个长方体玻璃容器 A 和 B(如图),在容器 B 中盛有 24 cm 高的水。如果把容器 B 中的一部分水倒进容器 A 中,使两个容器内水的高度一样,那么此时两个容器内水的高度是(
8
)cm。
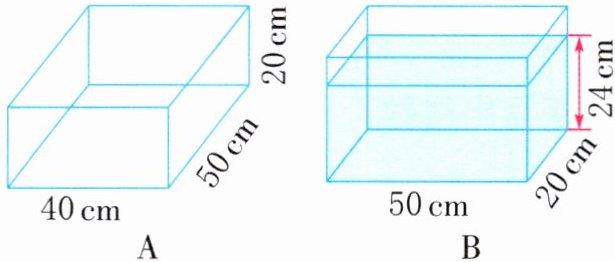
思路提示:水的总体积没变,两个容器内水的高度一样,用水的总体积除以两个容器底面积
的和。
答案:13. 8 解析:两个容器内水的高度一样,求两个容器内水的高度可以先计算出水的总体积和容器A、B的底面积之和,然后根据“长方体的高=体积÷底面积”求解即可。
解析:
水的总体积:$50×20×24 = 24000\,\mathrm{cm}^3$
容器A底面积:$40×50 = 2000\,\mathrm{cm}^2$
容器B底面积:$50×20 = 1000\,\mathrm{cm}^2$
底面积之和:$2000 + 1000 = 3000\,\mathrm{cm}^2$
此时水的高度:$24000÷3000 = 8\,\mathrm{cm}$
8