(1) 用(
100
)个边长为 1 厘米的小正方形可以拼成 1 个边长为 1 分米的大正方形;用(
1000
)个棱长为 1 厘米的小正方体可以拼成 1 个棱长为 1 分米的大正方体。
答案:1.(1)100 1000
(2) 从里面量得棱长为 1(
分米
)的正方体容器,可以装水 1000 毫升。
答案:1.(2)分米
(3) 一瓶药水共有 0.35 升,1 毫升药水约有 10 滴,这瓶药水大约一共有(
3500
)滴。
答案:1.(3)3500
解析:
0.35升=350毫升,350×10=3500滴。
(4) 如图,用 1 立方分米的正方体木块摆成一个长方体,正好能装满它右边的容器。该容器最多能装(
36
)升水。
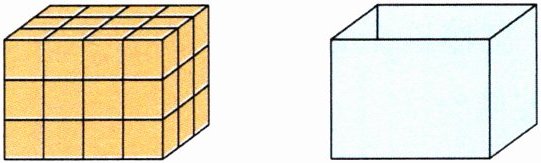
答案:1.(4)36
2. 单位换算。
6 $m^{3}$ = (
6000
) $dm^{3}$
4.8 $dm^{3}$ = (
4800
) $cm^{3}$
420 $dm^{3}$ = (
0.42
) $m^{3}$
82 $cm^{3}$ = (
0.082
) $dm^{3}$
4.7 $m^{3}$ = (
4700
)L
7800 mL = (
7800
) $cm^{3}$
1.6 $m^{3}$ = (
1600
) $dm^{3}$ = (
1600
)L
380 $cm^{3}$ = (
380
)mL = (
0.38
)L
8.06 $dm^{3}$ = (
8
)L(
60
)mL
答案:2.6000 4800 0.42 0.082 4700 7800 1600 1600 380 0.38 8 60
3. 一个底面周长是 200 厘米的正方体鱼缸,它的容积是多少升?(鱼缸的厚度忽略不计)
答案:3.200÷4=50(厘米)
50×50×50=125000(立方厘米)
125000立方厘米=125升
4. 将一堆砖摆成长方体形状,长 4 米,宽 20 分米,高 23 分米。如果每立方米有 500 块砖,那么这堆砖共有多少块?
答案:4.20分米=2米 23分米=2.3米
4×2×2.3×500=9200(块)
5. (生活体验)一个装有一些水的长方体玻璃缸,从里面量,长 20 cm,宽 10 cm,水深 4 cm。将一个体积是 1 $dm^{3}$ 的小石块浸没在水中,水未溢出。水面上升了多少厘米?
答案:5.1dm³=1000cm³ 1000÷(20×10)=5(cm)
解析:
1dm³=1000cm³
20×10=200(cm²)
1000÷200=5(cm)
6. (探究创新)如图所示为一张长方形铁皮,长 40 厘米,宽 30 厘米。从四个角都剪掉边长为 5 厘米的小正方形后,剩余部分可以焊成一个无盖的长方体盒子。这个长方体盒子最多能容纳多少升液体?
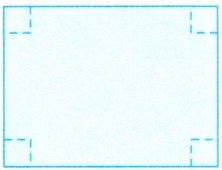
答案:6.40-2×5=30(厘米) 30-2×5=20(厘米) 30×20×5=3000(立方厘米) 3000立方厘米=3立方分米=3升
7. (思维过程)一个长方体(长、宽、高均为整分米数),相交于同一个顶点的三个面的面积分别是 15 平方分米、10 平方分米和 6 平方分米,把这个长方体切成棱长为 1 厘米的小正方体,可以切成(
30000
)个。
答案:7.30000 解析:长方体相交于同一个顶点的三个面的面积分别等于长×宽、长×高、宽×高,因为15=15×1=5×3,10=10×1=5×2,6=6×1=3×2,分析前面的算式可以知道长、宽、高分别是5分米、3分米、2分米,所以这个长方体的体积为5×3×2=30(立方分米)。因为30立方分米=30000立方厘米,所以可以切成30000个棱长为1厘米的小正方体。
解析:
设长方体的长、宽、高分别为$a$分米、$b$分米、$c$分米。相交于同一个顶点的三个面的面积分别为$ab = 15$平方分米,$ac = 10$平方分米,$bc = 6$平方分米。
因为$15 = 5×3$,$10 = 5×2$,$6 = 3×2$,所以$a = 5$分米,$b = 3$分米,$c = 2$分米。
长方体体积$V = abc = 5×3×2 = 30$立方分米。
因为$1$立方分米$= 1000$立方厘米,所以$30$立方分米$= 30×1000 = 30000$立方厘米。
棱长为$1$厘米的小正方体体积为$1$立方厘米,所以可切成小正方体的个数为$30000÷1 = 30000$个。
30000