2026年启东中学作业本八年级数学下册江苏版第4页解析答案

1. 在$□ ABCD$中，$BC$边上的高为$4$，$AB = 5$，$AC = 2\sqrt{5}$，则$□ ABCD$的周长为

12或20

答案：1. 12或20

解析：

解：分两种情况讨论：
情况一：高在BC边上
过点A作AE⊥BC于E，则AE=4。
在Rt△ABE中，AB=5，AE=4，
由勾股定理得：BE=$\sqrt{AB^2-AE^2}=\sqrt{5^2-4^2}=3$。
在Rt△AEC中，AC=$2\sqrt{5}$，AE=4，
由勾股定理得：EC=$\sqrt{AC^2-AE^2}=\sqrt{(2\sqrt{5})^2-4^2}=\sqrt{20-16}=2$。
此时BC=BE+EC=3+2=5，
周长=2(AB+BC)=2×(5+5)=20。
情况二：高在BC延长线上
过点A作AE⊥BC交BC延长线于E，则AE=4。
同理，BE=3，EC=2，
此时BC=BE-EC=3-2=1，
周长=2(AB+BC)=2×(5+1)=12。
综上，□ABCD的周长为12或20。

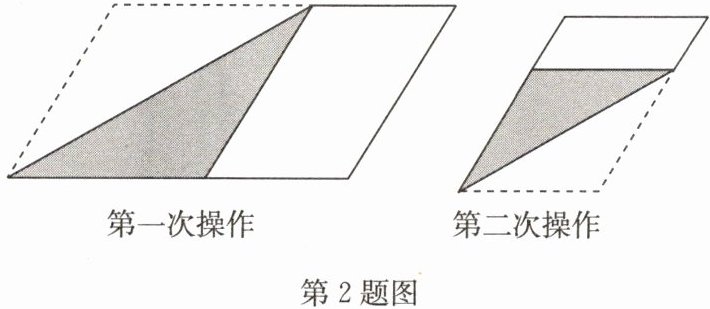
2. (2024·无锡天一实验中学期中)邻边长分别为$1$，$a(a ＞ 1)$的平行四边形纸片，如图那样折一下，剪下一个边长等于$1$的菱形(称为第一次操作)；再把剩下的平行四边形如图那样折一下，剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作)；再把剩下的平行四边形如此反复操作下去. 若在第三次操作后，剩下的平行四边形为菱形，则$a$的值为

$\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4

答案：
2. $\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4
点拨:①如答图①,经历三次折叠后，四边形IJHF为菱形。
∵四边形ABCD为菱形，
∴$AB = AD = BC = CD = 1$，
∴$DF = CE = a - 1$。
∵四边形GCEH为菱形，
∴$GC = CE = a - 1$，
∴$DG = FH = 1 - (a - 1) = 2 - a$。
∵四边形DGJI为菱形，
∴$DI = DG = 2 - a$，
∴$IF = a - 1 - (2 - a) = 2a - 3$。
∵四边形IJHF为菱形，
∴$IF = HF$，即$2a - 3 = 2 - a$，解得$a = \frac{5}{3}$；

②如答图②,经历三次折叠后，四边形DIHF为菱形。
∵四边形ABCD为菱形，
∴$AB = AD = BC = CD = 1$，
∴$DF = CE = a - 1$。
∵四边形JCEG，IJGH，DIHF都为菱形，
∴$DI = \frac{1}{3}CD = \frac{1}{3}$，
∴$a - 1 = \frac{1}{3}$，
解得$a = \frac{4}{3}$；

③如答图③,经历三次折叠后，四边形FIJH为菱形。
∵四边形ABCD，DCEF为菱形，
∴$AB = AD = BC = CD = CE = DF = EF = 1$，
∴$FH = a - 2$。
∵四边形FIJH，IEGJ都为菱形，
∴$FH = FI = IE = \frac{1}{2}EF = \frac{1}{2}$，
∴$a - 2 = \frac{1}{2}$，
解得$a = \frac{5}{2}$；

④如答图④,经历三次折叠后，四边形HGIJ为菱形。
∵四边形ABCD，DCEF，FEGH，HGIJ都为菱形，
∴$AB = AD = DF = FH = 1$，
∴$HJ = a - 3$，
∴$HJ = IJ$，
∴$a - 3 = 1$，解得$a = 4$。

综上，$a$的值为$\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4。

3. 如图，在$□ ABCD$中，$BD$为对角线，$EF$垂直平分$BD$，分别交$AD$，$BC$于点$E$，$F$，交$BD$于点$O$.
(1)求证：$BF = DE$；
(2)求证：$△ ABE≌△ CDF$；
(3)如果在$□ ABCD$中，$AB = 5$，$AD = 10$，有两动点$P$，$Q$分别从$B$，$D$两点同时出发，沿$△ BAE$和$△ DFC$各边运动一周，即点$P$自$B\rightarrow A\rightarrow E\rightarrow B$停止，点$Q$自$D\rightarrow F\rightarrow C\rightarrow D$停止，点$P$运动的路程是$m$，点$Q$运动的路程是$n$，当四边形$BPDQ$是平行四边形时，求$m$与$n$满足的数量关系.(画出示意图)

答案：
3. (1)证明:
∵四边形ABCD是平行四边形，
∴$AD // BC$，
∴$∠ ODE = ∠ OBF$。
∵EF垂直平分BD，
∴$OB = OD$。
在$△ OBF$和$△ ODE$中，$\begin{cases} ∠ OBF = ∠ ODE, \\ OB = OD, \\ ∠ BOF = ∠ DOE, \end{cases}$
∴$△ BOF ≌ △ DOE(ASA)$，
∴$BF = DE$。
(2)证明:
∵四边形ABCD是平行四边形，
∴$AB = CD$，$∠ A = ∠ C$，$AD = BC$。
∵$BF = DE$，
∴$AE = CF$。
在$△ ABE$和$△ CDF$中，$\begin{cases} AB = CD, \\ ∠ A = ∠ C, \\ AE = CF, \end{cases}$
∴$△ ABE ≌ △ CDF(SAS)$。
(3)解:
∵EF垂直平分BD，
∴$BF = DF$。
∵$△ ABE ≌ △ CDF$，
∴$BE = DF$，
∴$△ ABE$的周长是$BE + AE + AB = DE + AE + AB = AD + AB = 15$，$△ DFC$的周长也是15，分以下3种情况讨论:
①当点P在AB上，点Q在CD上时，如答图①。
∵$AB // CD$，
∴$∠ BPO = ∠ DQO$。
∵$∠ BOP = ∠ DOQ$，$OB = OD$，
∴$△ BPO ≌ △ DQO$，
∴$BP = DQ$，
∴$m + n = BP + DF + CF + CQ = DF + CF + CQ + DQ = DF + CF + CD = 15$；

②当点P在AE上，点Q在CF上时，如答图②。
∵$AD // BC$，
∴$∠ PEO = ∠ QFO$。
∵$△ EOD ≌ △ FOB$，
∴$OE = OF$。
又
∵$∠ EOP = ∠ FOQ$，
∴$△ PEO ≌ △ QFO$，
∴$PE = QF$。
∵$AE = CF$，
∴$CQ = AP$，
∴$m + n = AB + AP + DF + FQ = CD + CQ + DF + FQ = DF + CF + CD = 15$；
③当点P在BE上，点Q在DF上时，如答图③。
∵$DE = BF$，$DE // BF$，
∴四边形BEDF是平行四边形，
∴$OE = OF$，$BE // DF$，
∴$∠ PEO = ∠ QFO$。
∵$∠ EOP = ∠ FOQ$，
∴$△ PEO ≌ △ QFO$，
∴$PE = FQ$，
∴$m + n = AB + AE + PE + DQ = CD + CF + QF + DQ = DF + CF + CD = 15$。
综上，$m$与$n$的关系为$m + n = 15$。