11. 某学校评选出的寒假优质特色作业共分为四类:A(节日文化篇)、B(安全防疫篇)、C(劳动实践篇)、D(冬奥运动篇)。下面是根据统计结果绘制的两幅不完整的统计图,则B类作业所在扇形的圆心角是
72
度。
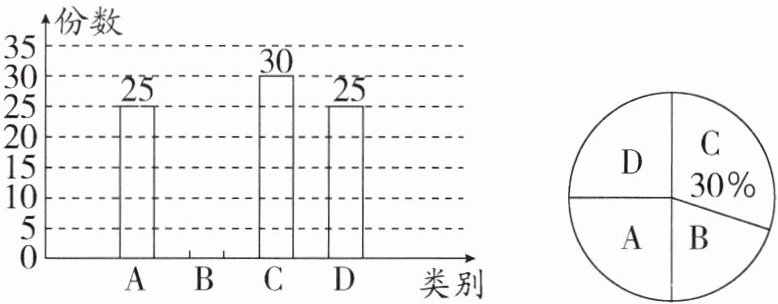
答案:11. 72 解析:优质特色作业共有 $ 30 ÷ 30\% = 100 $(份),B类作业有 $ 100 - 25 - 30 - 25 = 20 $(份),
∴B类作业所在扇形的圆心角是 $ 360^{\circ} × \dfrac{20}{100} = 72^{\circ} $。
12. 如图,在矩形ABCD中,AB=AO,对角线AC与BD相交于点O,以点A为圆心,以AO的长为半径作弧,交AD于点E,连接OE,则∠DOE=
45
°。
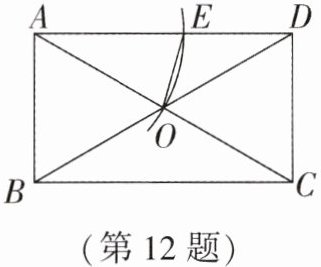
答案:12. 45 解析:
∵四边形 $ ABCD $ 是矩形,
∴ $ AC = BD $,$ AO = \dfrac{1}{2}AC $,$ OB = \dfrac{1}{2}BD $,
∴ $ OA = OB $。
∵ $ AB = AO $,
∴ $ △ AOB $ 是等边三角形,
∴ $ ∠ BAC = 60^{\circ} $。
∵ $ ∠ BAD = ∠ ADC = 90^{\circ} $,
∴ $ ∠ CAD = 30^{\circ} $。
∵ $ OA = OD $,
∴ $ ∠ ADO = ∠ DAO = 30^{\circ} $,
∴ $ ∠ AOD = 120^{\circ} $。
∵ $ AE = OA $,
∴ $ ∠ AOE = ∠ AEO = \dfrac{180^{\circ} - 30^{\circ}}{2} = 75^{\circ} $,
∴ $ ∠ DOE = ∠ AOD - ∠ AOE = 120^{\circ} - 75^{\circ} = 45^{\circ} $。
13. 某花木场有一块等腰梯形的空地ABCD(如图),各边的中点分别是E,F,G,H,用篱笆围成的四边形EFGH场地的周长为40cm,则对角线AC=
20
cm。
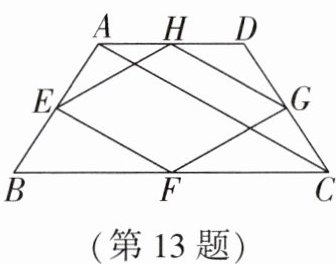
答案:13. 20 解析:连接 $ BD $,
∵等腰梯形的对角线相等,$ EF $,$ HG $,$ GF $,$ EH $ 均为三角形的中位线,
∴ $ EF = HG = GF = EH = \dfrac{1}{2}AC $。又
∵ $ EF + HG + GF + EH = 40\mathrm{cm} $,即 $ 2AC = 40\mathrm{cm} $,解得 $ AC = 20\mathrm{cm} $,
∴对角线 $ AC = 20\mathrm{cm} $。
14. 矩形ABCD中,AB=4,AD=5,E,F为直线AD上两点,且满足四边形BCFE为菱形,若M为EF的中点,则AM的长为
5.5 或 0.5
。
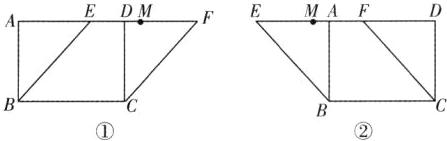
答案:14. 5.5 或 0.5 解析:分两种情况:第一种如图①所示。
∵四边形 $ ABCD $ 是矩形,
∴ $ CD = AB = 4 $,$ BC = AD = 5 $,$ ∠ ADC = ∠ CDF = 90^{\circ} $。
∵四边形 $ BCFE $ 为菱形,
∴ $ CF = EF = BE = BC = 5 $,
∴ $ DF = \sqrt{CF^2 - CD^2} = \sqrt{5^2 - 4^2} = 3 $,
∴ $ AF = AD + DF = 8 $。
∵ $ M $ 是 $ EF $ 的中点,
∴ $ MF = \dfrac{1}{2}EF = 2.5 $,
∴ $ AM = AF - MF = 8 - 2.5 = 5.5 $。第二种如图②所示,同理,得 $ AE = 3 $。
∵ $ M $ 是 $ EF $ 的中点,
∴ $ ME = 2.5 $,
∴ $ AM = AE - ME = 0.5 $。综上所述,线段 $ AM $ 的长为5.5或0.5.
15. (2025·泰州校级月考)如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=BQ,连接CP,QA,则PC+QA的最小值为
13
。
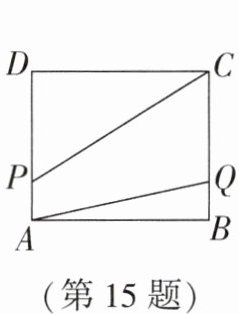
答案:15. 13 解析:如图,连接 $ BP $,$ PQ $,在矩形 $ ABCD $ 中,$ AD // BC $,$ ∠ PAB = 90^{\circ} $,
∴ $ AP // BQ $。
∵ $ AP = BQ $,
∴四边形 $ ABQP $ 是平行四边形。
∵ $ ∠ PAB = 90^{\circ} $,
∴四边形 $ ABQP $ 是矩形,
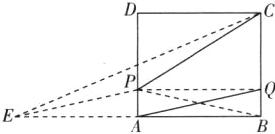
∴ $ QA = PB $,则 $ PC + QA = PC + PB $,则 $ PC + QA $ 的最小值转化为 $ PC + PB $ 的最小值。在 $ BA $ 的延长线上截取 $ AE = AB = 6 $,连接 $ PE $,
∵ $ PA ⊥ BE $,
∴ $ PA $ 是 $ BE $ 的垂直平分线,
∴ $ PB = PE $,
∴ $ PC + PB = PC + PE $。连接 $ CE $,则 $ PC + QA = PC + PB = PC + PE ≥ CE $。
∵ $ BE = 2AB = 12 $,$ BC = AD = 5 $,
∴ $ CE = \sqrt{BE^2 + BC^2} = 13 $。
∴ $ PC + QA $ 的最小值为13.
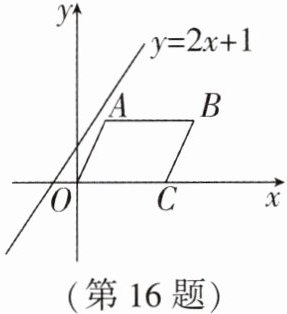
16. 如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过
6
秒该直线可将平行四边形OABC分成面积相等的两部分。
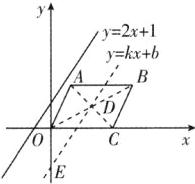
答案:16. 6 解析:连接 $ AC $,$ BO $ 交于点 $ D $,如图,当直线 $ y = 2x + 1 $ 向下平移经过 $ D $ 点时,与 $ y $ 轴的交点为 $ E $,直线 $ DE $ 可将 $ □ OABC $ 的面积平分。
∵四边形 $ OABC $ 是平行四边形,
∴ $ BD = OD $。由 $ B(6,2) $,易得 $ D(3,1) $。
∵直线 $ DE $ 是由直线 $ y = 2x + 1 $ 向下平移得到的,
∴设直线 $ DE $ 的表达式为 $ y = 2x + b $。
∵过 $ D(3,1) $,
∴ $ 2 × 3 + b = 1 $,解得 $ b = -5 $,
∴直线 $ DE $ 的表达式为 $ y = 2x - 5 $,
∴直线 $ y = 2x + 1 $ 要向下平移6个单位长度,即经过6秒该直线可将平行四边形 $ OABC $ 分成面积相等的两部分。
三、解答题(共72分)
17. (8分)(锦州中考)为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表。
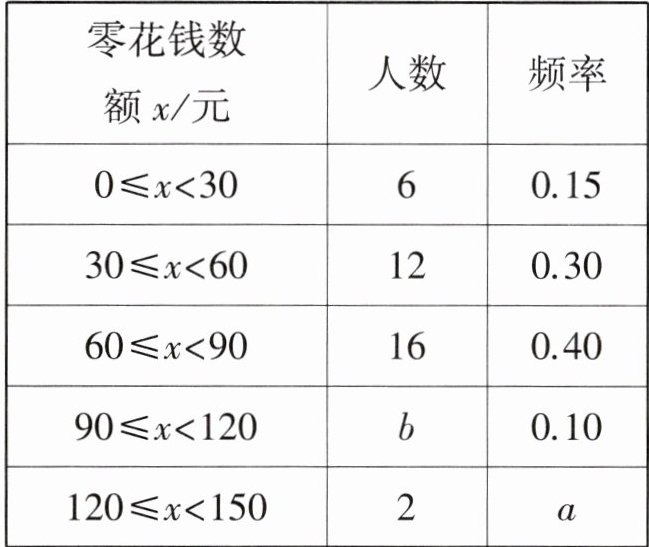
学生每月零花钱数额频数分布直方图
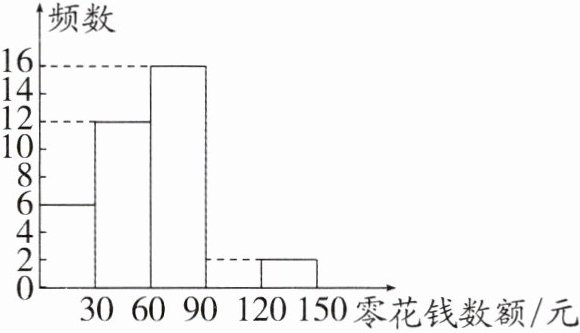
请根据以上图表,解答下列问题:
(1)这次被调查的人数共有
40
人,a=
0.05
;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90元的人数。
答案:17. (1) 40 0.05 解析:这次被调查的人数共有 $ 6 ÷ 0.15 = 40 $(人),则 $ a = 2 ÷ 40 = 0.05 $。
(2) $ b = 40 - 6 - 12 - 16 - 2 = 4 $,补全频数分布直方图如下:
学生每月零花钱数额频数分布直方图

(3)估计该校1500名学生中每月零花钱数额低于90元的人数为 $ 1500 × (0.15 + 0.30 + 0.40) = 1275 $(人)。