1. 下列调查中,不适合采用普查的是(
D
)
A.对进入地铁站的旅客携带物品的安检
B.调查我校七年级全体学生的入学数学成绩
C.学校招聘教师,对应聘人员的面试
D.调查长江水质情况
答案:1. D 解析:A.对进入地铁站的旅客携带物品的安检,重要程度高,适合采用普查;B.调查我校七年级全体学生的入学数学成绩,目的为调查全体学生情况,适合采用普查;C.学校招聘教师,对应聘人员的面试,适合采用普查;D.调查长江水质情况,适合采用抽样调查.故选 D.
2. (2025·酒泉期末)若多项式 $a^{2}+b^{2}+A$ 可以用平方差公式因式分解,则 $A$ 表示的单项式可以是(
D
)
A.$2bc$
B.$-2ab$
C.$3b^{2}$
D.$-5b^{2}$
答案:2. D 解析:形如 $ m^{2}-n^{2} $ 的式子可利用平方差公式因式分解,
∴当 $ A $ 表示的单项式为 $ -5b^{2} $ 时,$ a^{2}+b^{2}+A=a^{2}-4b^{2}=(a + 2b)·(a - 2b) $,符合题意.故选 D.
3. (赤峰中考)代数式 $\sqrt{3 - x}+\frac{1}{x - 1}$ 中 $x$ 的取值范围在数轴上表示为(
A
)
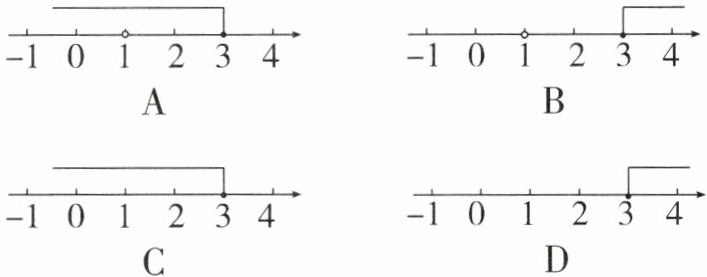
A.
B.
C.
D.
答案:3. A 解析:由题意可得 $ 3 - x≥0 $,$ x - 1≠0 $,$ \therefore x≤3 $ 且 $ x≠1 $,选项 A 的表示正确,故选 A.
4. 下列根式中,一定不是最简二次根式的是(
C
)
A.$\sqrt{2x + 1}$
B.$\sqrt{14}$
C.$\sqrt{0.5}$
D.$\frac{\sqrt{2b}}{4}$
答案:4. C 解析:$ \sqrt{0.5}=\sqrt{\dfrac{1}{2}}=\dfrac{\sqrt{2}}{2} $,一定不是最简二次根式.故选 C.
5. (2025·武汉期末)如图,在 $△ ABC$ 中,$AB = 10$,$BC = 6$,$D$ 为 $AB$ 上一点,$BC = BD$,$BE⊥ CD$ 于点 $E$,$F$ 为 $AC$ 的中点,连接 $EF$,则 $EF$ 的长为(
C
)
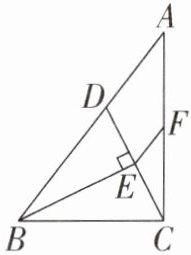
A.4
B.3
C.2
D.1
答案:5. C 解析:$ \because BD = BC = 6 $,$ \therefore AD = AB - BD = 4 $.$ \because BC = BD $,$ BE⊥ CD $,$ \therefore CE = ED $.又 $ F $ 为 $ AC $ 的中点,$ \therefore CF = FA $,$ \therefore EF=\dfrac{1}{2}AD = 2 $,故选 C.
6. (2025·漯河期末)高尔基说:“书,是人类进步的阶梯。”阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快。某中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A. 科普,B. 文学,C. 体育,D. 其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是(
A
)
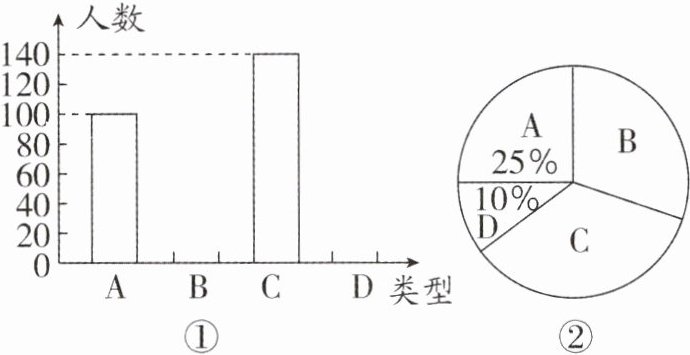
A.类型 $C$ 所占百分比为 $30\%$
B.类型 $D$ 所对应的扇形的圆心角为 $36^{\circ}$
C.样本容量为 400
D.类型 $B$ 的人数为 120
答案:6. A 解析:调查学生的总数为 $ 100÷25\% = 400 $(人),$ \therefore $ 类型 $ D $ 的人数为 $ 400×10\% = 40 $.类型 $ C $ 所占百分比为 $ \dfrac{140}{400}×100\% = 35\% $,故选项 A 说法错误;类型 $ D $ 所对应的扇形的圆心角为 $ \dfrac{40}{400}×360^{\circ}=36^{\circ} $,故选项 B 说法正确;样本容量为 400,故选项 C 说法正确;类型 $ B $ 的人数为 $ 400 - 100 - 140 - 40 = 120 $,故选项 D 说法正确.故选 A.
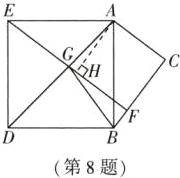
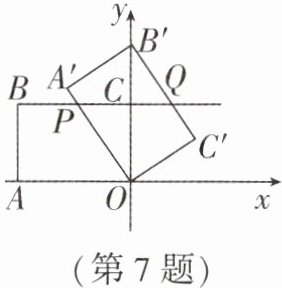
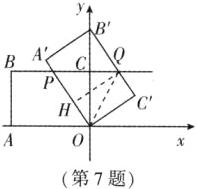
7. 如图,在平面直角坐标系中,点 $A$ 的坐标为 $(-8,0)$,点 $C$ 的坐标为 $(0,6)$,将矩形 $OABC$ 绕点 $O$ 按顺时针方向旋转 $α$ 得到矩形 $OA'B'C'$,此时直线 $OA'$,直线 $B'C'$ 分别与直线 $BC$ 相交于点 $P$,$Q$。当 $45^{\circ}<α≤90^{\circ}$,且 $BP = \frac{1}{2}BQ$ 时,线段 $PQ$ 的长是(
B
)
A.$\frac{4}{25}$
B.$\frac{25}{4}$
C.$\frac{25}{2}$
D.$\frac{2}{25}$
答案:7. B 解析:$ \because 45^{\circ}<α≤90^{\circ} $,$ \therefore $ 点 $ P $ 在点 $ B $ 的右侧.如图,过点 $ Q $ 作 $ QH⊥ OA' $ 于点 $ H $,连接 $ OQ $,则 $ QH = OC' = OC $.$ \because S_{△ POQ}=\dfrac{1}{2}PQ· OC=\dfrac{1}{2}OP· QH $,$ \therefore PQ = OP $.设 $ BP = x $,$ \because BP=\dfrac{1}{2}BQ $,$ \therefore BQ = 2x $,则 $ OP = PQ = BQ - BP = x $,$ PC = 8 - x $.在 $ \mathrm{Rt}△ PCO $ 中,根据勾股定理知,$ PC^{2}+OC^{2}=OP^{2} $,即 $ (8 - x)^{2}+6^{2}=x^{2} $,解得 $ x=\dfrac{25}{4} $,$ \therefore PQ = BP=\dfrac{25}{4} $.故选 B.
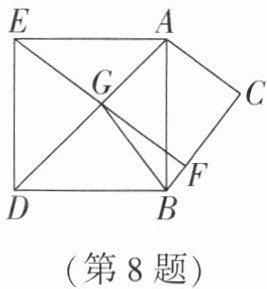
8. (2025·扬州期末)如图,在 $Rt△ ABC$ 中,$∠ C = 90^{\circ}$,$AC = 3$,$BC = 4$,以 $AB$ 为边在 $△ ABC$ 异侧作正方形 $ABDE$,过点 $E$ 作 $EF⊥ BC$,垂足为 $F$,$EF$ 交 $AD$ 于 $G$,连接 $BG$,则 $△ GBF$ 的周长等于(
B
)
A.6
B.8
C.10
D.12
答案:8. B 解析:过点 $ A $ 作 $ AH⊥ EF $ 于点 $ H $,$ \because $ 在 $ \mathrm{Rt}△ ABC $ 中,$ ∠ C = 90^{\circ} $,$ AC = 3 $,$ BC = 4 $,$ \therefore AB=\sqrt{AC^{2}+BC^{2}} = 5 $.$ \because ∠ C = 90^{\circ} $,$ EF⊥ CB $,$ AH⊥ EF $,$ \therefore $ 四边形 $ ACFH $ 为矩形,$ \therefore AC = FH = 3 $,$ ∠ CAH = 90^{\circ} $,$ \therefore ∠ BAC+∠ BAH = 90^{\circ} $.$ \because $ 四边形 $ ABDE $ 为正方形,$ \therefore AE = AB = 5 $,$ ∠ BAE = 90^{\circ} $,$ \therefore ∠ EAH+∠ BAH = 90^{\circ} $,$ \therefore ∠ EAH=∠ BAC $,在 $ △ ABC $ 和 $ △ AEH $ 中,
$ \begin{cases}∠ BAC=∠ EAH,\\∠ C=∠ AHE,\\AB = AE,\end{cases}$
$ \therefore△ ABC≌△ AEH(\mathrm{AAS}) $,$ \therefore EH = BC = 4 $,$ AC = AH = 3 $,$ \therefore CF = AH = 3 $,$ BF = BC - CF = 1 $,$ EF = EH + FH = 4 + 3 = 7 $.$ \because $ 四边形 $ ABDE $ 为正方形,$ \therefore ∠ EAG=∠ BAG $,$ AE = AB $.在 $ △ AEG $ 和 $ △ ABG $ 中,
$ \begin{cases}AG = AG,\\∠ EAG=∠ BAG,\\AE = AB,\end{cases}$
$ \therefore△ AEG≌△ ABG(\mathrm{SAS}) $,$ \therefore EG = BG $,$ \therefore △ BGF $ 的周长是 $ BF + BG + GF = BF + EG + GF = BF + EF = 1 + 7 = 8 $,故选 B.