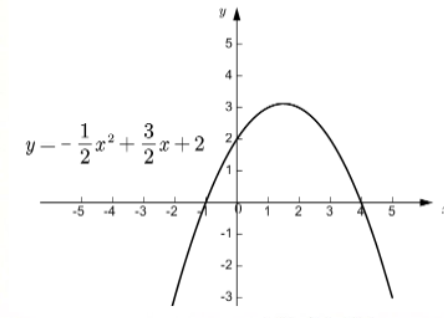
24. (10分)已知二次函数$y=ax^2+bx+c$的图像经过A、B、C三点,当$x≥0$时,其图像如图所示.
(1) 求该二次函数的函数表达式,并写出图像的顶点坐标;
(2) 画出当$x<0$时,二次函数$y=ax^2+bx+c$的图像;
(3) 根据图像,写出$x$为何值时,二次函数$y=ax^2+bx+c$的值大于0.

答案:解: (1)由图可知,抛物线过点(0,2),(4,0),(5,-3)
将点代入函数表达式得$\begin{cases}{c=2 }\\{4²×a+4b+c=0} \\{5²×a+5b+c=-3} \end{cases} $解得$\begin{cases}{a=-\dfrac {1}{2}}\\{b=\dfrac {3}{2}}\\{c=2}\end{cases}$
∴二次函数表达式为$y= -\frac {1}{2}x²+\frac {3}{2}x+ 2$
当$x=-\frac {b}{2a}=\frac {3}{2}$时,$y=\frac {25}{8}$
∴顶点坐标为$(\frac {3}{2},$$\frac {25}{8}) $
(2)如图所示
(3)由图可知,当-1<x<4时,y>0
25. (10分)如图,二次函数$y=\frac{1}{2}x^2-x+a$的图像与$x$轴交于点A、B,与$y$轴交于点C,其顶点在一次函数$y=-2x$的图像上.
(1) 求$a$的值.
(2) 求A、B两点的坐标.
(3) 以AC、CB为一组邻边作▱ACBD,则点D关于$x$轴的对称点$D'$是否在该二次函数的图像上?请说明理由.

答案:解: (1)二次函数的对称轴为$x=-\frac {b}{2a} = 1$
当x=1时,$y=a-\frac {1}{2}$
∵顶点在一次函数的图像上
∴顶点纵坐标为y=-2×1=-2
∴$a-\frac {1}{2}=-2$
∴$a=-\frac {3}{2}$
(2)二次函数表达式为$y=\frac {1}{2}x²-x-\frac {3}{2}$
令y=0,$\frac {1}{2}x²-x-\frac {3}{2}=0$
解得${x}_1=-1,$${x}_2=3$
∴A(-1,0),B(3,0)
(3)
∵四边形ACBD是平行四边形
∴点C、D关于对角线交点(1,0)对称
又
∵点D'是点D关于x轴的对称点
∴点C、D'关于抛物线的对称轴(直线x=1 )对称
∴点D'在二次函数图像上