1. $4$ 张质地、大小完全相同的卡片,正面分别画有圆、矩形、等边三角形、等腰梯形,背面图案都相同.现把它们正面向下摆放在桌面上,洗匀后从中任意抽出 $1$ 张,则抽出的卡片正面图案是中心对称图形的概率为(
B
).
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.$1$
答案:B
2. 如图,一只蚂蚁从点 $A$ 出发到 $D、E、F$ 处寻觅食物.假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如 $A$ 岔路口可以向左下到达 $B$ 处,也可以向右下到达 $C$ 处,其中 $A、B、C$都是岔路口).蚂蚁从点 $A$ 出发到达 $E$ 处的概率是
$\frac{1}{2}$
.

答案:$\frac {1}{2}$
3. 已知关于 $x$ 的一元二次方程 $x^2-x+k=0$,从$-2、-1、0、1、2$ 中任取一个数作为 $k$ 值,则所得的方程中有两个不相等的实数根的概率是
$\frac{3}{5}$
.
答案:$\frac {3}{5}$
4. 某班毕业联欢会上设计了摸球游戏:在一只不透明的盒子中,装有 $5$ 个分别标有数字 $1、2、3、4、5$ 的乒乓球,这些乒乓球除数字外,其他完全相同.参加联欢会的 $50$ 个同学,每人将盒子里的乒乓球摇匀后,从中随意摸出 $2$ 个球(每个同学必须且只能摸一次),记下数字后放回.若 $2$ 个球上的数字之和为偶数,则即兴表演一个节目;否则,下一个同学接着做摸球游戏,依次进行.
(1)用列表法或画树状图法求参加联欢会的某个同学即兴表演节目的概率;
(2)本次联欢会共进行了 $2 h$,每个同学摸球时间平均为 $30 s$,表演节目时间平均为 $150 s$,请你估计本次联欢会上有多少人表演节目.
答案:$\frac {3}{5}$
解: (1)游戏所有可能出现的结果如下表:
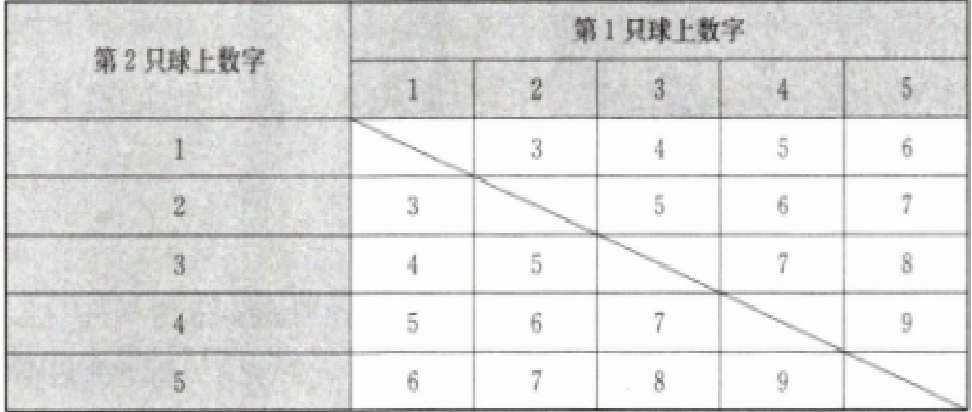
从上表可以看出,一次游戏共有20种等可能结果,其中两数和为偶数的共有8种。
∴P(两数和为偶数$)=\frac {8}{20}=\frac {2}{5}$
$(2)2×3600=7200(\mathrm {s})$
(7200-30×50)÷150=38(人)
答:估计本次联欢会上有38人表演节目。