14. 小华利用电能表和手表估测规格为“220 V 1100 W”的电水
壶的实际功率,电能表表盘如图所示。在此电水壶中加水,将其接入电
路,电能表脉冲指示灯在 3 min 内闪烁了 120 次。
(1)电路在 3 min 内消耗的电能是多少?
(2)电路的实际电功率是多大?
(3)电路实际电功率
大于
(选填“大于”“等于”或“小于”)电水
壶的额定功率。造成这一结果的原因是什么?

答案:14. (1) 0.1 kW·h (2) 2 000 W (3) 大于 家庭电路中其他用电器仍在工作
解析:
(1) 由电能表参数可知,$1200\ imp/(kW·h)$表示每消耗$1\ kW·h$的电能,脉冲指示灯闪烁$1200$次。
$3\ min$内闪烁$120$次,消耗的电能:
$W=\frac{120}{1200}\ kW·h=0.1\ kW·h$
(2) 时间$t=3\ min=0.05\ h$,实际电功率:
$P=\frac{W}{t}=\frac{0.1\ kW·h}{0.05\ h}=2\ kW=2000\ W$
(3) 大于 家庭电路中其他用电器仍在工作
15. 如图所示,灯泡 L 上标有“6 V 3 W”字样,电阻 R 的阻值为 12$\ \Omega$,当开关$S_1$闭合、$S_2$
拨至 a 点时,灯泡恰好正常发光。(不计温度对灯丝电阻的影响)
(1)求灯泡的电阻。
(2)求电源电压。
(3)当开关$S_1$闭合、$S_2$拨至 b 点时,灯泡的功率是多少瓦?
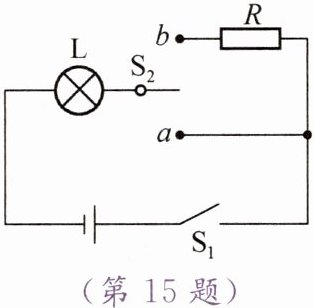
答案:15. (1) 12Ω (2) 6 V (3) 0.75 W
解析:
(1) 解:由 $P = \frac{U^2}{R}$ 得,灯泡的电阻:$R_L = \frac{U_L^2}{P_L} = \frac{(6\ V)^2}{3\ W} = 12\ \Omega$
(2) 解:当开关$S_1$闭合、$S_2$拨至$a$点时,电路为灯泡$L$的简单电路,灯泡恰好正常发光,所以电源电压$U = U_L = 6\ V$
(3) 解:当开关$S_1$闭合、$S_2$拨至$b$点时,灯泡$L$与电阻$R$串联,电路总电阻$R_{ 总} = R_L + R = 12\ \Omega + 12\ \Omega = 24\ \Omega$,电路中的电流$I = \frac{U}{R_{ 总}} = \frac{6\ V}{24\ \Omega} = 0.25\ A$,灯泡的功率$P_L' = I^2 R_L = (0.25\ A)^2 × 12\ \Omega = 0.75\ W$
1. 如图所示是我们在测量额定电压已知的灯泡的额定功率时所采用的电路图。在这个实验的操作中,应移动滑动变阻器的滑片,同时 (
C
)
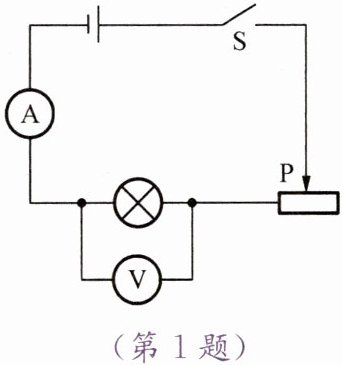
A.观察变阻器滑片的位置
B.观察灯泡是否发光
C.观察电压表的示数
D.观察电流表的示数
答案:1. C