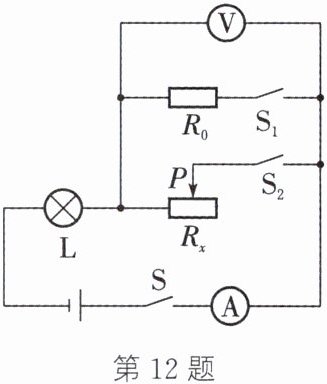
12.(2024·常州)如图所示的电路中,电源电压恒定,小灯泡 L 标有“$ 6 V \quad 3.6 W $”字样(忽略温度变化对灯丝电阻的影响),滑动变阻器 $ R_x $ 标有“$ 200 \Omega \quad 1.25 A $”字样,定值电阻 $ R_0 $ 阻值为 $ 20 \Omega $,电流表的量程为 $ 0 \sim 3 A $,电压表的量程为 $ 0 \sim 15 V $。
(1)求小灯泡的额定电流。
(2)求小灯泡的电阻。
(3)只闭合开关 $ S $、$ S_1 $,小灯泡恰好正常发光,求电源电压。
(4)只闭合开关 $ S $、$ S_2 $,在保证电路元件安全的前提下,求滑动变阻器接入电路的电阻范围。
答案:12. (1) 小灯泡的额定电流$I_{额} = \frac{P_{额}}{U_{额}} = \frac{3.6\ W}{6\ V} = 0.6\ A$ (2) 小灯泡的电阻$R_{L} = \frac{U_{额}}{I_{额}} = \frac{6\ V}{0.6\ A} = 10\ \Omega$ (3) 只闭合开关S、S₁,L 与R₀ 串联,小灯泡恰好正常发光,电路中电流$I = I_{额} = 0.6\ A$,电源电压$U = I(R_0 + R_{L}) = 0.6\ A×(20\ \Omega + 10\ \Omega) = 18\ V$ (4) 只闭合 S、S₂ 时,L 与Rₓ 串联,滑动变阻器Rₓ 上标有“200 Ω 1.25 A”的字样,电流表A 的量程为0~3 A,小灯泡的额定电流为0.6 A,因串联电路中电流处处相等,则为了保护电路的安全,电路中的最大电流$I_{最大} = I_{额} = 0.6\ A$,此时小灯泡正常发光,则电压表的最小示数$U_{x最小} = U - U_{额} = 18\ V - 6\ V = 12\ V < 15\ V$,不会损坏电压表,变阻器Rₓ 的最小阻值$R_{x最小} = \frac{U_{x最小}}{I_{最大}} = \frac{12\ V}{0.6\ A} = 20\ \Omega$;当滑片向右滑动时,其接入电路的电阻变大,电流变小,根据分压原理,变阻器两端电压即电压表示数变大,由于电压表使用的量程为0~15 V,可得$U_{x最大} = 15\ V$,此时电路中的最小电流$I_{最小} = \frac{U - U_{x最大}}{R_{L}} = \frac{18\ V - 15\ V}{10\ \Omega} = 0.3\ A$,变阻器Rₓ 的值$R_{x最大} = \frac{U_{x最大}}{I_{最小}} = \frac{15\ V}{0.3\ A} = 50\ \Omega$,故滑动变阻器Rₓ 能接入电路的阻值范围是20~50 Ω
解析:
(1)解:小灯泡的额定电流$I_{额}=\frac{P_{额}}{U_{额}}=\frac{3.6\ W}{6\ V}=0.6\ A$
(2)解:小灯泡的电阻$R_{L}=\frac{U_{额}}{I_{额}}=\frac{6\ V}{0.6\ A}=10\ \Omega$
(3)解:只闭合开关$S$、$S_{1}$,$L$与$R_{0}$串联,小灯泡正常发光,电路中电流$I = I_{额}=0.6\ A$,电源电压$U=I(R_{0}+R_{L})=0.6\ A×(20\ \Omega + 10\ \Omega)=18\ V$
(4)解:只闭合$S$、$S_{2}$时,$L$与$R_{x}$串联,电路最大电流$I_{最大}=I_{额}=0.6\ A$,此时$U_{x最小}=U - U_{额}=18\ V-6\ V=12\ V$,$R_{x最小}=\frac{U_{x最小}}{I_{最大}}=\frac{12\ V}{0.6\ A}=20\ \Omega$;电压表示数最大$U_{x最大}=15\ V$,电路最小电流$I_{最小}=\frac{U - U_{x最大}}{R_{L}}=\frac{18\ V-15\ V}{10\ \Omega}=0.3\ A$,$R_{x最大}=\frac{U_{x最大}}{I_{最小}}=\frac{15\ V}{0.3\ A}=50\ \Omega$,故滑动变阻器接入电路的电阻范围是$20\ \Omega\sim50\ \Omega$