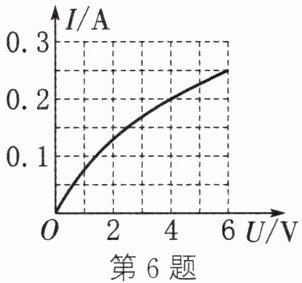
6. (2025·常州模拟)标有“$6 V \ \ 1.5 W$”的灯泡,通过它的电流随其两端电压变化的物理图像如图所示,若把这只灯泡与一个$20\Omega$的定值电阻串联起来,接在电压为$8 V$的电源两端。则下列说法中正确的是 (
D
)
A.此时电路中的电流为$0.25 A$
B.此时定值电阻$R$两端的电压为$2 V$
C.此时灯泡的实际电功率为$1.5 W$
D.此时整个电路的总电阻为$40\Omega$
答案:6.D
解析:
解:设电路中电流为$I$,灯泡两端电压为$U_L$,定值电阻$R=20\Omega$,电源电压$U=8V$。
由串联电路特点:$U=U_L+IR$,即$8V=U_L+I×20\Omega$,得$U_L=8V - 20\Omega× I$。
结合图像,当$I=0.2A$时,$U_L=4V$,满足$4V=8V - 20\Omega×0.2A$。
A. 电路中电流为$0.2A\neq0.25A$,A错误。
B. 定值电阻两端电压$U_R=IR=0.2A×20\Omega=4V\neq2V$,B错误。
C. 灯泡实际功率$P_L=U_LI=4V×0.2A=0.8W\neq1.5W$,C错误。
D. 电路总电阻$R_{总}=\frac{U}{I}=\frac{8V}{0.2A}=40\Omega$,D正确。
答案:D
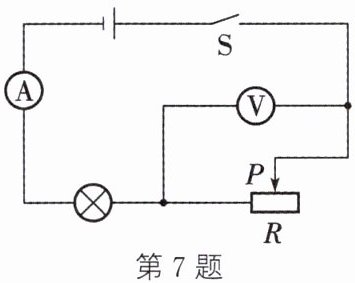
7. 将标有“$2 V \ \ 1 W$”字样的小灯泡(灯丝电阻不变)和标有“$20\Omega \ \ 1 A$”字样的滑动变阻器连接在如图所示的电路图中,其中电源两端电压恒为$4.5 V$,电流表量程为$0∼0.6 A$,电压表量程为$0∼3 V$。闭合开关,为保证电路安全,在移动滑动变阻器滑片的过程中,下列说法正确的是 (
A
)
A.电流表示数变化范围是$0.375∼0.5 A$
B.电压表示数变化范围是$2.4∼3 V$
C.滑动变阻器阻值变化范围是$5∼20\Omega$
D.电路的最大功率是$2.7 W$
答案:7.A
解析:
解:
1. 小灯泡电阻:$R_{L}=\frac{U_{L}^{2}}{P_{L}}=\frac{(2\ V)^{2}}{1\ W}=4\ \Omega$,额定电流:$I_{L}=\frac{P_{L}}{U_{L}}=\frac{1\ W}{2\ V}=0.5\ A$
2. 电路最大电流$I_{max}=0.5\ A$(灯泡额定电流限制),此时:
总电阻$R_{总}=\frac{U}{I_{max}}=\frac{4.5\ V}{0.5\ A}=9\ \Omega$
滑动变阻器最小阻值$R_{min}=R_{总}-R_{L}=9\ \Omega-4\ \Omega=5\ \Omega$
电压表示数$U_{R}=U-I_{max}R_{L}=4.5\ V-0.5\ A×4\ \Omega=2.5\ V$
3. 电压表示数最大$U_{Rmax}=3\ V$时:
灯泡电压$U_{L}'=U-U_{Rmax}=4.5\ V-3\ V=1.5\ V$
电路最小电流$I_{min}=\frac{U_{L}'}{R_{L}}=\frac{1.5\ V}{4\ \Omega}=0.375\ A$
滑动变阻器最大阻值$R_{max}=\frac{U_{Rmax}}{I_{min}}=\frac{3\ V}{0.375\ A}=8\ \Omega$
4. 结论:
电流表示数范围:$0.375\ A~0.5\ A$
电压表示数范围:$2.5\ V~3\ V$
滑动变阻器阻值范围:$5\ \Omega~8\ \Omega$
电路最大功率$P_{max}=UI_{max}=4.5\ V×0.5\ A=2.25\ W$
A
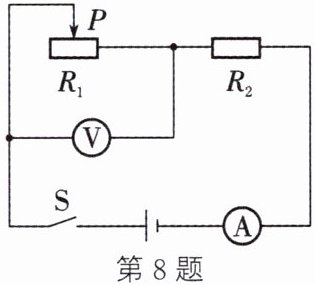
8. 如图所示的电路中,电源电压保持$6 V$不变,滑动变阻器的最大阻值为$15\Omega$,定值电阻$R_2$为$5\Omega$。电压表示数为$U_1$、$R_2$的电功率为$P_2$、电流表示数为$I$。闭合开关后,移动滑片$P$,下列图像可能正确的是 (
D
)

答案:8.D
解析:
由电路图可知,滑动变阻器与定值电阻$R_2$串联,电压表测滑动变阻器两端电压$U_1$,电流表测电路电流$I$。
电源电压$U = 6V$,$R_2=5\Omega$,滑动变阻器最大阻值$R_{滑max}=15\Omega$。
电路总电阻$R = R_{滑}+R_2$,电流$I=\frac{U}{R}=\frac{6V}{R_{滑}+5\Omega}$。
$U_1 = IR_{滑}=\frac{6V× R_{滑}}{R_{滑}+5\Omega}=\frac{6V}{\frac{R_{滑}+5\Omega}{R_{滑}}}=\frac{6V}{1+\frac{5\Omega}{R_{滑}}}$,$U_1$随$R_{滑}$增大而增大,当$R_{滑}=0$时,$U_1=0$;当$R_{滑}=15\Omega$时,$U_1=\frac{6V×15\Omega}{15\Omega + 5\Omega}=4.5V$。
$P_2 = I^{2}R_2=(\frac{6V}{R_{滑}+5\Omega})^{2}×5\Omega$,$P_2$随$R_{滑}$增大而减小,当$R_{滑}=0$时,$P_2=(\frac{6V}{5\Omega})^{2}×5\Omega=7.2W$;当$R_{滑}=15\Omega$时,$P_2=(\frac{6V}{20\Omega})^{2}×5\Omega=0.45W$。
分析图像,只有选项D符合上述关系。
D
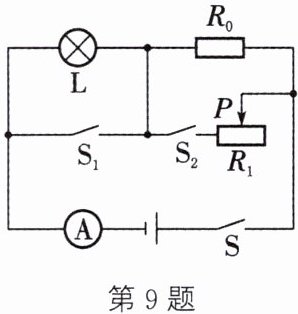
9. (2024·南通二模)如图所示的电路中,电源电压恒定,小灯泡 L 标有“$3 V \ \ 3 W$”字样,定值电阻$R_0$阻值为$6\Omega$,滑动变阻器$R_1$的规格是“$20\Omega \ \ 1 A$”,电流表所选量程为$0∼3 A$。只闭合开关$S$,小灯泡正常发光。求:
(1)小灯泡的额定电流。
(2)电源电压。
(3)三个开关都闭合,在确保电路安全的情况下,电路 1 min 内最多消耗的电能。
答案:9.(1)小灯泡的额定电流$ I_L=\frac{P_L}{U_L}=\frac{3W}{3V}=1A$
(2)闭合开关S,小灯泡正常发光,此时电路中小灯泡L与电阻R₀串联,电阻R₀两端的电压U₀=$I_L$R₀=1A×6Ω=6V;电源电压U=U₀+$U_L$=6V+3V=9V
(3)三个开关都闭合,小灯泡L被短路,电路中R₀和R₁并联,电流表测量干路电流,此时通过R₀的电流$I₀=\frac{U}{R_0}=\frac{9V}{6Ω}=1.5A;$
最大干路电流$I_{总max}=I₀+I_{1max}=1.5A+1A=2.5A<3A;$
在确保电路安全的情况下,电路1min内最多消耗的电能$W_{max}=UI_{总max}t=9V×2.5A×60s=1350J$