1. 一旗杆在离地面 $ 6 $ m 处折断,旗杆顶部落在离旗杆底部 $ 8 $ m 处,旗杆折断之前有多高?
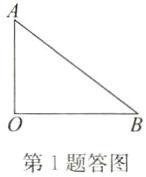
答案:解:如答图,设旗杆在A处折断,落地点B离旗杆底部O 的距离OB=8m,则OA=6m
在Rt△AOB中,由勾股定理,得AB²=6²+8²=100,解得AB=10.
∵OA+AB=6+10=16(m),
∴旗杆折断之前高16m.
2. 一艘轮船以 $ 24 $ 海里/时的速度离开港口向东南方向航行,另一艘轮船同时以 $ 10 $ 海里/时的速度离开港口向西南方向航行,经过 $ 1 $ 小时,这两艘轮船相距多远?
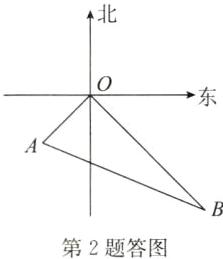
答案:解:如答图,由题意得OA=10×1=10(海里),OB=24×1=24(海里).
∵东南方向与西南方向垂直,
∴∠AOB=90°,
∴AB²=OA²+OB²=10²+24²=676.
∴AB=26(海里).
答:经过1小时,这两艘轮船相距26海里.
3. 老师准备测量一段河水的深度,他把一根竹竿插到离岸边 $ 1.5 $ 米远的水底,竹竿露出水面的部分刚好 $ 0.5 $ 米,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,请你帮老师计算河水的深度.
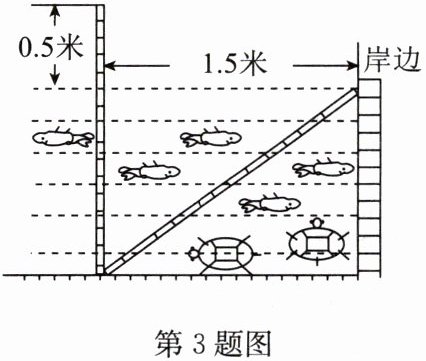
答案:解:设河水的深度是x米,则竹竿高(x+0.5)米.
根据题意,得1.5²+x²=(x+0.5)²,解得x=2.
答:河水的深度是2米.
4. 如图,在离水面高度为 $ 8 $ m 的岸上,有人用绳子拉船靠岸,开始时绳子 $ BC $ 的长为 $ 17 $ m,几分钟后船到达点 $ D $ 的位置,此时绳子 $ CD $ 的长为 $ 10 $ m,问船向岸边移动了多少米?
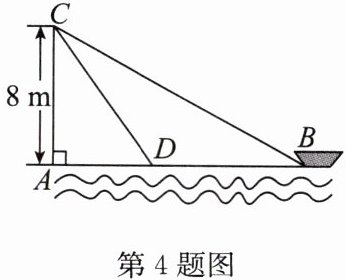
答案:解:在Rt△ABC中,由勾股定理,得AB²=BC²-AC²=17²-8²=15²,解得AB=15.
在Rt△ACD中,由勾股定理,得AD²=CD²-AC²=10²-8²=6²,解得AD=6.
∴DB=AB-AD=15-6=9(m).
答:船向岸边移动了9m.