1. 已知一次函数的图象经过点$(-2,-7)和点(2,5)$,求该一次函数的表达式以及函数图象与坐标轴的交点坐标.
答案:解:设该一次函数的表达式为y=kx+b,根据题意,得{-2k+b=-7,2k+b=5},解得{k=3,b=-1}.
∴该一次函数的表达式为y=3x−1. 在y=3x−1中,令x=0,得y=−1;令y=0,得x=$\frac{1}{3}$.
∴该函数图象与坐标轴的交点坐标为($\frac{1}{3}$,0),(0,−1).
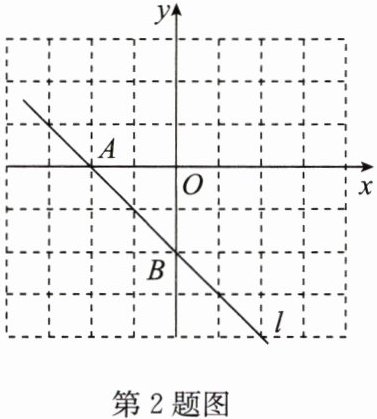
2. 如图,直线$l经过点A(-2,0)$,$B(0,-2)$,将该直线向右平移$2个单位长度得到直线l'$.
(1)在图中画出直线$l'$;
(2)求直线$l'$的函数表达式.
答案:解:
(1)如答图,直线l'即为所求.
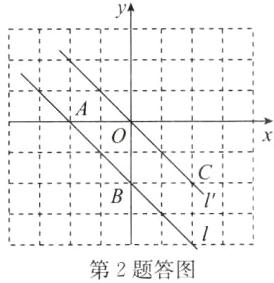
(2)
∵点A(2,0),B(0,−2)向右平移2个单位长度后的坐标分别为O(0,0),C(2,−2),如答图,
∴直线l'经过O,C两点 设其函数表达式为y=kx,则2k=−2,解得k=−1.
∴直线l'的函数表达式为y=−x.
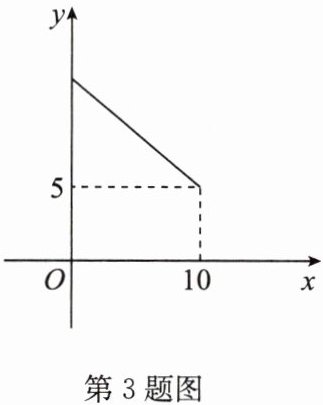
3. 如图是小林画出的函数$y = -\dfrac{1}{2}x + 10$的部分图象,利用图象回答:
(1)自变量$x$的取值范围;
(2)当$x$取何值时,$y$取得最大值、最小值?最小值、最大值各是多少?
(3)在图中,当$x$增大时,$y$的值是怎样变化的?
答案:解:
(1)由题图可知0≤x≤10.
(2)由题图及已知条件可知,当x=0时,y取最大值,为10;当x=10时,y取最小值,为5.
(3)
∵k=−$\frac{1}{2}$<0,
∴y随x的增大而减小.
4. 已知函数$y = -2x + 3$.
(1)画出这个函数的图象;
(2)写出函数与$x$轴的交点坐标,与$y$轴的交点坐标;
(3)求此函数的图象与坐标轴围成的三角形的面积.
答案:解:
(1)这个函数的图象如答图所示,
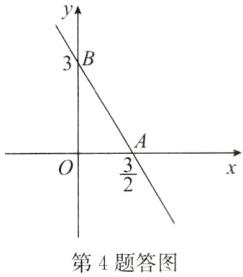
(2)由答图可知,该函数的图象与x轴的交点坐标为A($\frac{3}{2}$,0),与y轴的交点坐标为B(0,3).
(3)
∵A($\frac{3}{2}$,0),B(0,3),
∴OA=$\frac{3}{2}$,OB=3,
∴S△AOB=$\frac{1}{2}$OA·OB=$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$.
∴此函数的图象与坐标轴围成的三角形的面积为$\frac{9}{4}$.