1. 一次函数 $ y = kx + b $($ k $,$ b $ 为常数,$ k \neq 0 $)的图象是
一条直线
,通常取点$(0,$
b
$)和点($
$-\frac{b}{k}$
$,0)$画图.
答案:一条直线 b $-\frac{b}{k}$
2. 一次函数 $ y = kx + b $ 的图象可以由正比例函数
$y=kx$(k为常数,$k≠0$)
的图象沿 $ y $ 轴向
上
$(b > 0)$或向
下
$(b < 0)$平移 $ |b| $ 个单位长度得到.
答案:$y=kx$(k为常数,$k≠0$) 上 下
解析:
$y=kx$($k$为常数,$k\neq0$) 上 下
1. 一次函数 $ y = -x + 5 $ 的图象不经过(
C
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:C
解析:
对于一次函数$y = -x + 5$,其中$k=-1$,$b=5$。
因为$k=-1\lt0$,$b=5\gt0$,所以函数图象经过第一、二、四象限,不经过第三象限。
C
2. 点$(3,-5)$在一次函数 $ y = kx + 1 $($ k \neq 0 $)的图象上,则 $ k $ 的值为(
A
)
A.$-2$
B.$2$
C.$-3$
D.$3$
答案:A
解析:
因为点$(3,-5)$在一次函数$y = kx + 1$的图象上,所以将$x=3$,$y=-5$代入函数可得:$-5 = 3k + 1$,解得$3k=-5 - 1=-6$,$k=-2$。
A
3. 若函数 $ y = (m - 1)x^{|m|} + m $ 是一次函数,则该函数的图象不经过第
一
象限.
答案:一
解析:
因为函数$y=(m - 1)x^{|m|} + m$是一次函数,所以$\begin{cases}|m|=1\\m - 1\neq0\end{cases}$。
由$|m|=1$得$m=\pm1$,由$m - 1\neq0$得$m\neq1$,所以$m=-1$。
则函数为$y=(-1 - 1)x^{|-1|} + (-1)=-2x - 1$。
因为$k=-2\lt0$,$b=-1\lt0$,所以该函数的图象经过第二、三、四象限,不经过第一象限。
一
4. 若一次函数 $ y = kx + b $ 的图象与正比例函数 $ y = 2x $ 的图象平行,且经过点 $ A(1,-2) $,则 $ kb = $
-8
.
答案:-8
解析:
解:因为一次函数$y = kx + b$的图象与正比例函数$y = 2x$的图象平行,所以$k = 2$。
又因为一次函数经过点$A(1,-2)$,将$x = 1$,$y = -2$,$k = 2$代入$y = kx + b$,得$-2 = 2×1 + b$,解得$b = -4$。
所以$kb = 2×(-4) = -8$。
$-8$
5. 将一次函数 $ y = 2x + 1 $ 的图象沿 $ y $ 轴向下平移 $ 3 $ 个单位长度后,得到的直线的函数表达式为
$y=2x-2$
.
答案:$y=2x-2$
解析:
解:一次函数$y = 2x + 1$的图象沿$y$轴向下平移$3$个单位长度,根据函数图象平移规律“上加下减”,得到的直线函数表达式为$y = 2x + 1 - 3$,即$y = 2x - 2$。
$y=2x-2$
6. 如图,在同一平面直角坐标系中画出下列函数的图象,并指出它们的共同之处.
(1) $ y = 4x $;
(2) $ y = 4x + 1 $;
(3) $ y = -4x + 1 $;
(4) $ y = -4x - 1 $.
答案:解:画函数图象如答图所示.
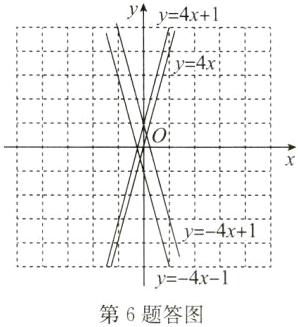
函数$y=4x$的图象与函数$y=4x+1$的图象平行;函数$y=-4x+1$的图象与函数$y=-4x-1$的图象平行.