1. 用描点法画正比例函数的图象,步骤是
列表
、
描点
、
连线
。
答案:列表 描点 连线
2. 正比例函数 $ y = kx $($ k $ 为常数,$ k \neq 0 $)的图象是
一条经过原点的直线
,因此画正比例函数的图象,只需描出图象上除原点以外的另一个点。
答案:一条经过原点的直线
3. 正比例函数 $ y = kx $($ k $ 为常数,$ k \neq 0 $)具有以下图象特征和性质:
答案: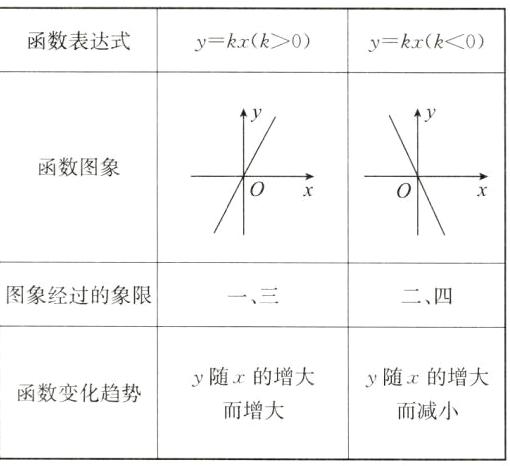
1. 正比例函数 $ y = -2x $ 的大致图象是(
C
)
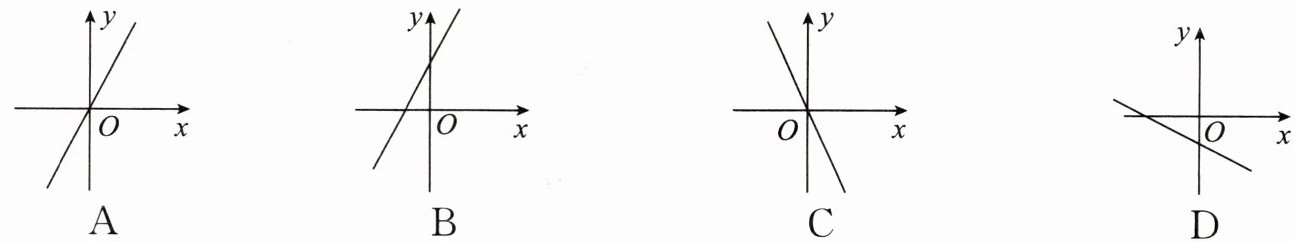
答案:C
解析:
解:正比例函数$y = -2x$,其中$k=-2<0$,所以函数图象经过第二、四象限,且过原点。
观察选项,C选项的图象符合上述特征。
C
2. 正比例函数 $ y = kx(k \neq 0) $ 的图象经过点 $ (-2025, 2025) $,则 $ k $ 的值是(
A
)
A.$ -1 $
B.$ \pm 1 $
C.$ 1 $
D.$ -2025 $
答案:A
解析:
将点$(-2025, 2025)$代入$y = kx$,得$2025 = k×(-2025)$,解得$k=-1$。
A
3. 正比例函数 $ y = 3x $ 的图象经过的象限是(
A
)
A.第一、三象限
B.第二、四象限
C.第三、四象限
D.第一、二象限
答案:A
解析:
对于正比例函数$y = kx$($k$为常数,$k\neq0$),当$k>0$时,函数图象经过第一、三象限。
在函数$y = 3x$中,$k = 3>0$,所以其图象经过第一、三象限。
A
4. 正比例函数 $ y = (m - 6)x $,$ y $ 随 $ x $ 的增大而增大,那么 $ m $ 的取值范围是(
B
)
A.$ m < 6 $
B.$ m > 6 $
C.$ m < -6 $
D.$ m > -6 $
答案:B
解析:
对于正比例函数$y = kx$($k$为常数,$k\neq0$),当$k>0$时,$y$随$x$的增大而增大。
在函数$y=(m - 6)x$中,$k = m - 6$,因为$y$随$x$的增大而增大,所以$m - 6>0$,解得$m>6$。
B
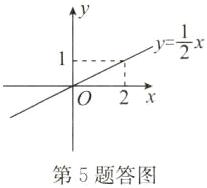
5. 在平面直角坐标系中画出函数 $ y = \frac{1}{2}x $ 的图象。
答案:解:函数y=$\frac{1}{2}$x的图象如答图所示.