1. 平面内两条互相垂直的
数轴
构成平面直角坐标系,简称为
直角坐标系
. 水平的数轴称为
x
轴或
横
轴,向
右
为正方向;竖直方向的数轴称为
y
轴或
纵
轴,向
上
为正方向,两轴的交点 $O$ 称为
原点
.
答案:数轴 直角坐标系 x 横 右 y 纵 上 原点
2. 点 $P$ 在平面直角坐标系中,过点 $P$ 分别作 $x$ 轴、$y$ 轴的垂线,垂足在 $x$ 轴、$y$ 轴上表示的数分别为 $a$,$b$,则点 $P$ 的坐标为
(a,b)
,其中 $a$ 称为
横
坐标,$b$ 称为
纵
坐标.
答案:(a,b) 横 纵
3. 在平面直角坐标系中,原点的坐标为
(0,0)
.
答案:(0,0)
5. 在平面直角坐标系中,两条坐标轴将平面分成的四个区域称为象限,按逆时针顺序分别记为第
一
、
二
、
三
、
四
象限,其内部的点的坐标的符号分别为 $(+,+)$、
$(-,+)$
、
$(-,-)$
、
$(+,-)$
. 坐标轴不属于任何象限.
答案:一 二 三 四 (+,+) (-,+) (-,-) (+,-)
1. 下列各点中,在第四象限的点是(
C
)
A.$(2,0)$
B.$(-2,3)$
C.$(2,-3)$
D.$(-2,-3)$
答案:C
解析:
第四象限的点的坐标特征是横坐标为正,纵坐标为负。
A.$(2,0)$在x轴上,不符合;
B.$(-2,3)$横坐标为负,纵坐标为正,在第二象限,不符合;
C.$(2,-3)$横坐标为正,纵坐标为负,在第四象限,符合;
D.$(-2,-3)$横坐标为负,纵坐标为负,在第三象限,不符合。
C
2. 点 $(2,3)$,$(2,-3)$,$(1,0)$,$(0,-3)$,$(0,0)$,$(-2,3)$ 中,不属于任何象限的有(
C
)
A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$4$ 个
答案:C
解析:
在平面直角坐标系中,坐标轴上的点不属于任何象限。坐标轴上的点满足横坐标为0或纵坐标为0。
点$(2,3)$:横、纵坐标均不为0,在第一象限;
点$(2,-3)$:横、纵坐标均不为0,在第四象限;
点$(1,0)$:纵坐标为0,在x轴上,不属于任何象限;
点$(0,-3)$:横坐标为0,在y轴上,不属于任何象限;
点$(0,0)$:横、纵坐标均为0,是坐标原点,不属于任何象限;
点$(-2,3)$:横、纵坐标均不为0,在第二象限。
不属于任何象限的点有$(1,0)$,$(0,-3)$,$(0,0)$,共3个。
C
3. 若点 $P(-2,a)$ 在第二象限,则 $a$ 的值可以是(
A
)
A.$1$
B.$-1$
C.$0$
D.$-2$
答案:A
解析:
第二象限内点的坐标特征为横坐标小于0,纵坐标大于0。
点$P(-2,a)$在第二象限,横坐标$-2<0$,则纵坐标$a>0$。
选项中只有$1>0$。
A
4. 在平面直角坐标系中,点 $M$ 在第四象限,且到 $x$ 轴、$y$ 轴的距离分别为 $6$,$4$,则点 $M$ 的坐标为
(4,-6)
.
答案:(4,-6)
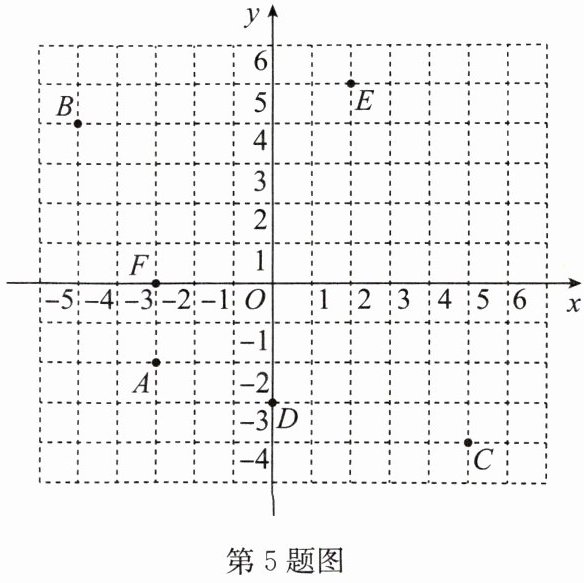
5. (1) 如图,写出点 $A$,$B$,$C$,$D$,$E$,$F$ 的坐标;
(2) 在图中描出下列各点:$L(-5,-3)$,$M(4,0)$,$N(0,5)$,$P(6,2)$.
答案:解:
(1)A(-3,-2),B(-5,4),C(5,-4),D(0,-3),E(2,5),F(-3,0).
(2)如答图.