用勾股定理去探究一些学科内的综合问题,常需找(或构造出)
直角
三角形.
答案:直角
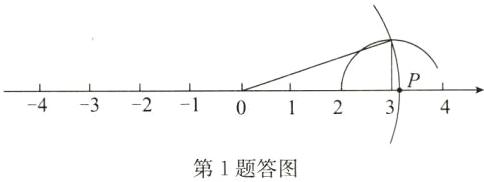
1. 如图,请在数轴上画出表示$\sqrt{10}的点P$.

答案:解:如答图,点P即为所求.
2. 如图,在$\triangle ABC$中,$AD\perp BC$,垂足为$D$. 求证:$AB^{2}-AC^{2}= BD^{2}-CD^{2}$.
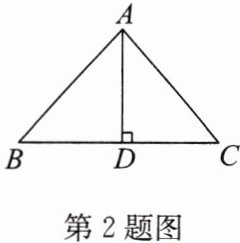
答案:证明:
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∴AB²=AD²+BD²,AC²=AD²+CD².
∴AB²−AC²=(AD²+BD²)−(AD²+CD²),即AB²−AC²=BD²−CD².
3. 如图,在四边形$ABCD$中,$AC\perp BD$,垂足为$O$. 若$AD = 5$,$BC = 2$,求$AB^{2}+CD^{2}$的值.
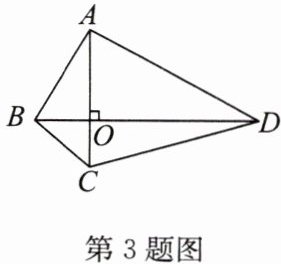
答案:解:
∵AC⊥BD,
∴∠AOB=∠AOD=∠BOC=∠COD=90°.
∴AB²=OA²+OB²,AD²=OA²+OD²,BC²=OB²+OC²,CD²=OC²+OD².
∴AB²+CD²=OA²+OB²+OC²+OD²,AD²+BC²=OA²+OB²+OC²+OD².
∴AB²+CD²=AD²+BC².
∵AD=5,BC=2,
∴AB²+CD²=5²+2²=29.