1. 如图,$AB = BE$,$\angle DBC= \frac{1}{2}\angle ABE$,$BD\perp AC$,则下列结论:①$CB平分\angle DCE$;②$\angle ABE+\angle DCE = 180^{\circ}$;③$AC = 2BE + CE$;④$AC = 2CD - CE$. 其中正确的结论为( )
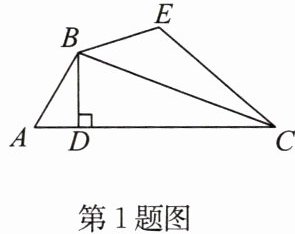
A.①②③
B.①②④
C.②③④
D.①③④
答案:1.B 点拨:如答图,延长CD,以点B为圆心,BC长为半径画弧,交CD的延长线于点F,连接BF,则BF=BC,过点B作BG⊥CE,交CE的延长线于点G.
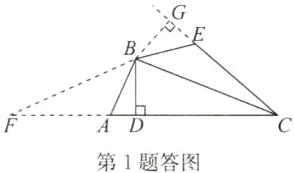
∵FB=BC,BD⊥AC,
∴DF=DC,∠DBC=∠DBF=$\frac{1}{2}$∠FBC.
∵∠DBC=$\frac{1}{2}$∠ABE,
∴∠FBC=∠ABE,
∴∠FBA=∠CBE.
在△FAB和△CEB中,$\left\{\begin{array}{l} AB=EB,\\ ∠FBA=∠CBE,\\ BF=BC,\end{array}\right. $
∴△FAB≌△CEB(SAS).
∴∠F=∠BCE,AF=CE.
∵BF=BC,
∴∠F=∠BCD.
∴∠BCD=∠BCE,
∴CB平分∠DCE.故①正确.
∵∠FBC+∠F+∠BCD=180°,
∴∠ABE+∠BCE+∠BCD=180°.
∴∠ABE+∠DCE=180°.故②正确.
在△BDC和△BGC中,$\left\{\begin{array}{l} ∠BDC=∠BGC=90^{\circ },\\ ∠BCD=∠BCG,\\ BC=BC,\end{array}\right. $
∴△BDC≌△BGC(AAS).
∴BD=BG,CD=CG.
在Rt△BDA和Rt△BGE中,$\left\{\begin{array}{l} AB=EB,\\ BD=BG,\end{array}\right. $
∴Rt△BDA≌Rt△BGE(HL).
∴AD=GE.
∵AC=AD+DC,
∴AC=AD+CG=AD+GE+CE=2GE+CE.
∵GE≠BE,
∴AC≠2BE+CE.故③错误.
∵AC=CF - AF,
∴AC=2CD - CE.故④正确.
综上,正确的结论为①②④.故选B.