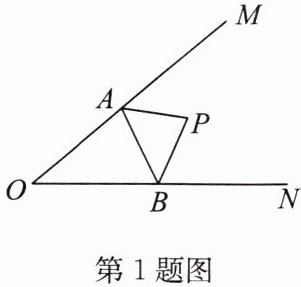
1. 如图,$\angle MON = 40^{\circ}$,$P为\angle MON$内一点,$A为OM$上一点,$B为ON$上一点,当$\triangle PAB$的周长取最小值时,$\angle APB$的度数为( )
A.$40^{\circ}$
B.$80^{\circ}$
C.$100^{\circ}$
D.$140^{\circ}$
答案:1.C 点拨:如答图,分别作点P关于OM,ON的对称点P',P'',连接OP,OP',OP'',连接P'P''分别交OM,ON 于点A,B,连接PA,PB,此时△PAB的周长最小,最小值等于P'P''长.
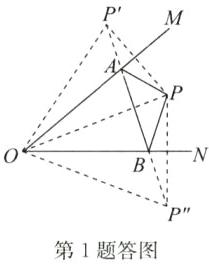
由轴对称性质可得,OP'=OP''=OP,∠P'OA=∠POA,∠P''OB=∠POB,
∴∠P'OP''=2∠MON=2×40°=80°.
∴∠OP'P''=∠OP''P'=(180°−80°)÷2=50°.
又
∵∠BPO=∠BP''O=50°,∠APO=∠AP'O=50°,
∴∠APB=∠APO+∠BPO=100°.故选C.