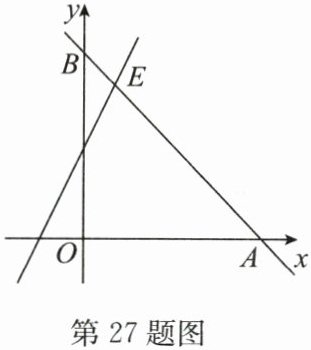
2025年启东中学作业本八年级数学上册苏科版宿迁专版第162页解析答案

27. (12分)如图,一次函数$y_{1}= -x+5的图象与x$轴、$y轴分别交于点A$,$B$,一次函数$y_{2}= mx+m(m＞0)的图象与图象y_{1}交于点E(1,n)$.
(1)求点$E的坐标及m$的值;
(2)当$-x+5\geq mx+m$时,直接写出$x$的取值范围;
(3)若点$P在一次函数y_{2}$的图象上,且$S_{\triangle AEP}= 3$,求点$P$的坐标.

答案：
（1）解:由题意知n=-1+5=4,
∴E(1,4).
　
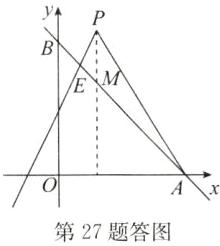
∴m+m=4,解得m=2.　　综上,点E的坐标为(1,4),m的值为2.　　（2）x≤1.　　（3）如答图,过点P作PM//y轴交AB于点M,　　设P(t,2t+2),则M(t,-t+5),
　
∴PM=|2t+2-(-t+5)|=|3t-3|.
　
∵直线y=-x+5与x轴交于点A(5,0),$S_{\triangle AEP}=3$,　　　　　　　

　
∴$\frac{1}{2}$×PM×|$x_{A}-x_{E}$|=3,　　即$\frac{1}{2}$×|3t-3|×|5-1|=3,
∴t=$\frac{1}{2}$或t=$\frac{3}{2}$.
　
∴P($\frac{1}{2}$,3)或P($\frac{3}{2}$,5)即为所求.

28. (12分)定义:在平面直角坐标系中,对于任意一次函数$y= kx+b(k\neq 0)$的图象,作该图象在直线$x= m的右侧部分关于直线x= m$的轴对称图形,与原图象在直线$x= m的右侧部分及与直线x= m$的交点共同构成一个新函数的图象,则这个新函数叫作原函数关于直线$x= m$的“V型函数”.例如:图①就是一次函数$y= x+2关于直线x= -1$的“V型函数”图象.
(1)请在图②中画出函数$y= x+2关于直线x= 0$的“V型函数”图象;
(2)若函数$y= x+10关于直线x= m$的“V型函数”图象与$x$轴只有一个交点,则$m= $______;
(3)如图③,点$C(-12,0)$,以$OC为斜边在x轴上方作等腰Rt\triangle COB$,当函数$y= x+10关于直线x= m$的“V型函数”图象与$\triangle COB$的边只有两个交点时,求$m$的取值范围.

答案：
（1）解:函数y=x+2关于直线x=0的“V型函数”图象如答图①所示.

（2）-10 （3）解:
∵等腰Rt△COB中,C(-12,0),
∴OC=12,B(-6,6),
∴直线OB的函数表达式为y=-x.解方程x+10=-x得x=-5.由
(2)知直线y=x+10与x轴的交点为(-10,0),
∴当-10＜m＜-5时,函数y=x+10关于直线x=m 的“V型函数”图象与△COB的边只有两个交点,
∵直线y=x+10与△COB的边已经有两个交点,
∴函数y=x+10关于直线x=m的"V型函数"图象与△COB的边不能再有交点,即在点C(-12,0)的左侧.
∴C(-12,0)与点(-10,0)关于x=m对称.
∴如答图②,当m=-11时,函数y=x+10关于直线x=m的"V型函数"图象经过点C(-12,0).
∴当函数y=x+10关于直线x=m的“V型函数"图象与△COB的边只有两个交点时，m的取值范围是-10＜m＜-5或m＜-11.　　　　　　