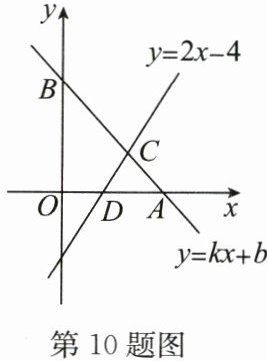
10. (14 分)如图,已知直线 $ y = kx + b $ 交 $ x $ 轴于点 $ A $,交 $ y $ 轴于点 $ B $,直线 $ y = 2x - 4 $ 交 $ x $ 轴于点 $ D $,交直线 $ AB $ 于点 $ C(3,2) $.
(1) 根据图象写出关于 $ x $ 的不等式 $ 2x > kx + b + 4 $ 的解集;
(2) 若点 $ A $ 的坐标为 $ (5,0) $,求直线 $ AB $ 的函数表达式;
(3) 在(2)的条件下,求四边形 $ BODC $ 的面积.
答案:解:
(1)原不等式可转化为$2x-4>kx+b$,根据图象可得不等式的解集为$x>3.$
(2)把$(5,0),(3,2)$代入$y=kx+b$,可得$\left\{\begin{array}{l} 5k+b=0,\\ 3k+b=2,\end{array}\right. $解得$\left\{\begin{array}{l} k=-1,\\ b=5,\end{array}\right. $
∴直线 AB 的函数表达式为$y=-x+5.$
(3)把$x=0$代入$y=-x+5$得$y=5$,
∴点$B(0,5),$把$y=0$代入$y=2x-4$得$x=2,$
∴点$D(2,0),\therefore DA=3,$$\therefore S_{四边形BODC}=S_{\triangle AOB}-S_{\triangle ACD}=\frac {1}{2}×5×5-\frac {1}{2}×3×2=9.5.$
11. (12 分)(2024·宿城期末)如图,在 $ \triangle ADF $ 和 $ \triangle BCE $ 中,点 $ B $,$ F $,$ E $,$ D $ 依次在一条直线上.若 $ AF // CE $,$ \angle B = \angle D $,$ BF = DE $,求证:$ AF = CE $.
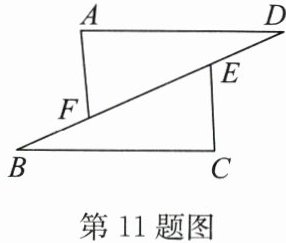
答案:证明:$\because AF// CE,\therefore ∠AFD=∠CEB.$$\because BF=DE,\therefore BF+EF=EF+DE$,即$BE=DF.$又$\because ∠B=∠D,\therefore \triangle ADF\cong \triangle CBE(ASA).$$\therefore AF=CE.$
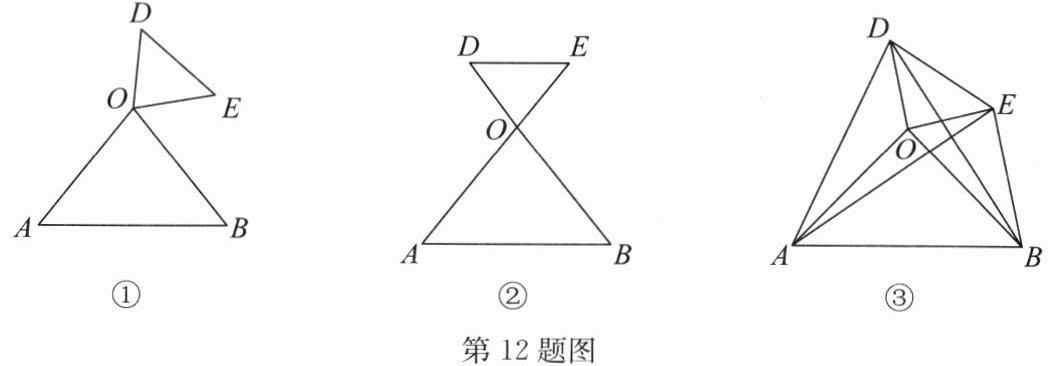
12. (16 分)定义:两个顶角相等且顶角顶点重合的等腰三角形称为“同根等腰三角形”,如图①,$ OD = OE $,$ OA = OB $,$ O $ 为重合的顶角顶点且 $ \angle DOE = \angle AOB $,所以 $ \triangle ODE $ 与 $ \triangle OAB $ 是“同根等腰三角形”.
(1) 将图①的 $ \triangle ODE $ 绕点 $ O $ 旋转,使点 $ D $ 在线段 $ BO $ 的延长线上,如图②,求证:$ DE // AB $;
(2) 如图③,$ \triangle ODE $ 与 $ \triangle OAB $ 是“同根等腰三角形”,且 $ \angle DOE = \angle AOB = 90^{\circ} $,连接 $ AE $,$ BD $,试探究 $ AE $ 和 $ BD $ 的位置关系,并说明理由;
(3) 在图③中,连接 $ BE $,$ AD $.若 $ OD = 3 $,$ OA = 5 $,$ \angle BED = 135^{\circ} $,求 $ AD^2 $ 的值.
答案:
(1)证明:
∵点 D 在线段 BO 的延长线上,
∴B,O,D 三点共线.由"同根等腰三角形"的定义知$∠AOB=∠DOE.$又$\because OD=OE,OA=OB,\therefore ∠D=∠E,∠A=∠B,$$\because 180^{\circ }-∠DOE=180^{\circ }-∠AOB,$$\therefore 2∠D=2∠B,$即$∠D=∠B,\therefore DE// AB.$
(2)解:$AE⊥BD$,理由如下:设 AE 交 OB 于点 F,交 BD 于点 G,如答图①.$\because ∠DOE=∠AOB=90^{\circ },$$\therefore ∠DOE+∠BOE=∠AOB+∠BOE,$即$∠BOD=∠AOE.$在$\triangle BOD$和$\triangle AOE$中,$\left\{\begin{array}{l} OD=OE,\\ ∠BOD=∠AOE,\\ OB=OA,\end{array}\right. $$\therefore \triangle BOD\cong \triangle AOE(SAS).$$\therefore ∠OBD=∠OAE.$$\because ∠BFG=∠AFO,$$\therefore 180^{\circ }-∠OBD-∠BFG=180^{\circ }-∠OAE-∠AFO,$即$∠BGF=∠AOF.$$\because ∠AOF=90^{\circ },\therefore AE⊥BD.$
(3)解:过点 D 作$DK⊥BE$,交 BE 的延长线于点 K,如答图②.$\because ∠DOE=90^{\circ },OD=OE=3,$$\therefore ∠DEO=45^{\circ },DE=3\sqrt {2}.$$\because ∠BED=135^{\circ },$$\therefore ∠BEO=∠BED-∠DEO=135^{\circ }-45^{\circ }=90^{\circ },$$∠DEK=180^{\circ }-∠BED=180^{\circ }-135^{\circ }=45^{\circ }.$$\because OA=OB=5,\therefore BE=\sqrt {OB^{2}-OE^{2}}=\sqrt {5^{2}-3^{2}}=4.$由$DK⊥BE,∠DEK=45^{\circ }$,可得$\triangle DEK$是等腰直角三角形,$\therefore DK=EK=3.$$\therefore BK=EK+BE=3+4=7.$在$Rt\triangle BDK$中,$BD=\sqrt {BK^{2}+DK^{2}}=\sqrt {7^{2}+3^{2}}=\sqrt {58}$,由
(2)知$\triangle BOD\cong \triangle AOE,$$\therefore AE=BD=\sqrt {58}.$设$GB=x$,则$GD=\sqrt {58}-x.$由
(1)知$∠EGB=90^{\circ }=∠DGE,$$\therefore BE^{2}-BG^{2}=GE^{2}=DE^{2}-GD^{2},$$\therefore 16-x^{2}=(3\sqrt {2})^{2}-(\sqrt {58}-x)^{2},$解得$x=\frac {14\sqrt {58}}{29}$,即$GB=\frac {14\sqrt {58}}{29}.$$\therefore GD=\sqrt {58}-x=\frac {15\sqrt {58}}{29},GE=\sqrt {BE^{2}-GB^{2}}=$$\sqrt {16-(\frac {14\sqrt {58}}{29})^{2}}=\frac {6\sqrt {58}}{29}.$$\therefore GA=AE-GE=\sqrt {58}-\frac {6\sqrt {58}}{29}=\frac {23\sqrt {58}}{29}.$在$Rt\triangle AGD$中,$AD^{2}=GD^{2}+GA^{2}=(\frac {15\sqrt {58}}{29})^{2}+$$(\frac {23\sqrt {58}}{29})^{2}=52.\therefore AD^{2}$的值是 52.