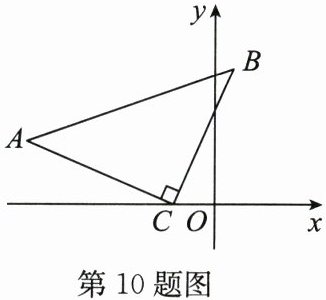
10. (2024·江阴期末)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ},AC = BC$. 若点$C(-2,0),A(-6,3)$,则点$B$的坐标是
(1,4)
.
答案:(1,4)
解析:
解:设点$B$的坐标为$(x,y)$。
$\because$点$C(-2,0)$,$A(-6,3)$,
$\therefore AC$的斜率$k_{AC}=\dfrac{3 - 0}{-6 - (-2)}=\dfrac{3}{-4}=-\dfrac{3}{4}$,
$BC$的斜率$k_{BC}=\dfrac{y - 0}{x - (-2)}=\dfrac{y}{x + 2}$。
$\because \angle ACB = 90^{\circ}$,
$\therefore AC\perp BC$,则$k_{AC}\cdot k_{BC}=-1$,
即$-\dfrac{3}{4}\cdot\dfrac{y}{x + 2}=-1$,化简得$3y = 4(x + 2)$,即$4x - 3y + 8 = 0$。①
$\because AC = BC$,
$\therefore AC^{2}=(-6 + 2)^{2}+(3 - 0)^{2}=16 + 9 = 25$,
$BC^{2}=(x + 2)^{2}+(y - 0)^{2}=(x + 2)^{2}+y^{2}$,
$\therefore (x + 2)^{2}+y^{2}=25$。②
联立①②,由①得$x=\dfrac{3y - 8}{4}$,代入②:
$\left(\dfrac{3y - 8}{4}+ 2\right)^{2}+y^{2}=25$,
$\left(\dfrac{3y}{4}\right)^{2}+y^{2}=25$,
$\dfrac{9y^{2}}{16}+y^{2}=25$,
$\dfrac{25y^{2}}{16}=25$,
$y^{2}=16$,解得$y = 4$或$y=-4$。
当$y = 4$时,代入①得$4x - 12 + 8 = 0$,$4x = 4$,$x = 1$;
当$y=-4$时,代入①得$4x + 12 + 8 = 0$,$4x=-20$,$x=-5$(舍去,由图知$B$在第一象限附近)。
$\therefore$点$B$的坐标为$(1,4)$。
$(1,4)$
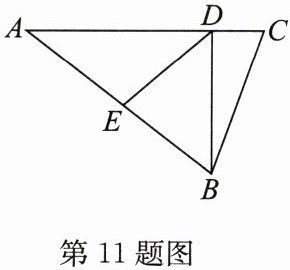
11. (15分)如图,在$\triangle ABC$中,$AC = 21,BC = 13,D是AC$边上一点,$BD = 12,AD = 16$.
(1)求证:$BD \perp AC$;
(2)若$E是边AB$上的动点,求线段$DE$长度的最小值.
答案:
(1)证明:
∵AC=21,AD=16,
∴CD=AC-AD=5.
∵BD²+CD²=12²+5²=169=BC²,
∴∠BDC=90°,
∴BD⊥AC.
(2)解:当DE⊥AB时,线段DE长度的值最小.由
(1)知△ABD是直角三角形,
∴AB=√(AD²+BD²)=√(16²+12²)=20.又
∵(1/2)AD·DB=(1/2)AB·DE,
∴DE=(16×12)/20=9.6,
∴线段DE长度的最小值为9.6.
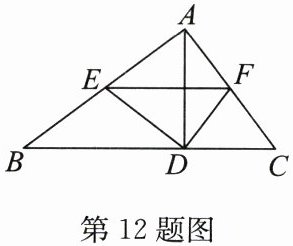
12. (15分)如图,在$\triangle ABC$中,$AD$是高,$E,F分别是AB,AC$的中点,$AB = 8,AC = 6$.
(1)求四边形$AEDF$的周长.
(2)$EF与AD$有怎样的位置关系? 证明你的结论.
(3)
12
四边形$AEDF$面积的最大值是______.
答案:
(1)解:在△ABC中,AD是高,E,F分别是AB,AC的中点,
∴DE=(1/2)AB=AE,DF=(1/2)AC=AF.
∵AB=8,AC=6,
∴四边形AEDF的周长=AE+DE+AF+DF=AB+AC=8+6=14.
(2)解:EF⊥AD,理由:
∵AE=DE,AF=DF,
∴点E,F都在线段AD的垂直平分线上.
∴直线EF垂直平分线段AD,即EF⊥AD.
(3)12
13. (20分)如图,长方形$OABC$是一张放在平面直角坐标系中的长方形纸片,$O$为坐标原点,点$A在x$轴上,点$C在y$轴上,$OA = 10,OC = 6$. 在$AB上取一点M$,使得$\triangle CBM沿CM$翻折后,点$B落在x$轴上,记作点$B'$.
(1)点$B'$的坐标是
(8,0)
.
(2)求折痕$CM$所在直线的函数表达式.
解:设AM=x,则BM=AB-AM=6-x.∵OA=10,B'O=8,∴B'A=2.∵△CBM沿CM翻折,∴B'M=BM=6-x.在Rt△AB'M中,B'A²+AM²=B'M²,∴2²+x²=(6-x)²,解得x=8/3,∴M(10,8/3).设折痕CM所在直线的函数表达式为y=kx+b,将(0,6),(10,8/3)代入得{6=b,{8/3=10k+b,解得{k=-1/3,{b=6,∴折痕CM所在直线的函数表达式为y=-1/3x+6.
(3)在$x轴上是否存在一点P$,使$\triangle B'CP的面积为12$? 若存在,求出点$P$的坐标;若不存在,请说明理由.
解:存在.∵△B'CP的面积为12,∴(1/2)B'P·OC=12,∴(1/2)B'P×6=12,∴B'P=4,∵B'(8,0),∴P(12,0)或P(4,0).
答案:
(1)(8,0)
(2)解:设AM=x,则BM=AB-AM=6-x.
∵OA=10,B'O=8,
∴B'A=2.
∵△CBM沿CM翻折,
∴B'M=BM=6-x.在Rt△AB'M中,B'A²+AM²=B'M²,
∴2²+x²=(6-x)²,解得x=8/3,
∴M(10,8/3).设折痕CM所在直线的函数表达式为y=kx+b,将(0,6),(10,8/3)代入得{6=b,{8/3=10k+b,解得{k=-1/3,{b=6,
∴折痕CM所在直线的函数表达式为y=-1/3x+6.
(3)解:存在.
∵△B'CP的面积为12,
∴(1/2)B'P·OC=12,
∴(1/2)B'P×6=12,
∴B'P=4,
∵B'(8,0),
∴P(12,0)或P(4,0).