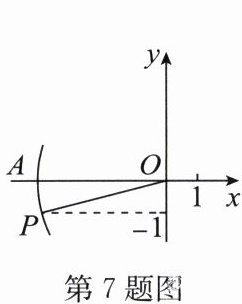
7. 如图,在平面直角坐标系中,以点$O$为圆心,以$OP$的长为半径画弧,交$x轴的负半轴于点A$,点$A的坐标为(-\sqrt{26},0)$,点$P的纵坐标为-1$,则点$P$的坐标为
(-5,-1)
.
解析:
解:
∵以点$O$为圆心,以$OP$的长为半径画弧,交$x$轴的负半轴于点$A$,
∴$OA = OP$。
∵点$A$的坐标为$(-\sqrt{26},0)$,
∴$OA=\sqrt{26}$,则$OP = \sqrt{26}$。
设点$P$的坐标为$(x,-1)$,
∵点$P$在平面直角坐标系中,
∴由勾股定理得$x^{2}+(-1)^{2}=OP^{2}$,
即$x^{2}+1 = 26$,
$x^{2}=25$,
解得$x=\pm5$。
∵点$P$在第三象限(由图可知点$P$的横坐标为负),
∴$x=-5$,
∴点$P$的坐标为$(-5,-1)$。
$(-5,-1)$