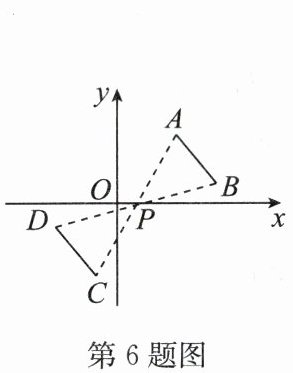
6. (2024·镇江期末)如图,线段 $ AB $ 与线段 $ CD $ 关于点 $ P $ 对称,若 $ A(3,3) $,$ B(5,1) $,$ D(-3,-1) $,则点 $ C $ 的坐标为 (
B
)
A.$ (-3,-3) $
B.$ (-1,-3) $
C.$ (-4,-2) $
D.$ (-2,-4) $
解析:
解:设点$P$的坐标为$(x,y)$,点$C$的坐标为$(a,b)$。
因为线段$AB$与线段$CD$关于点$P$对称,所以点$P$是线段$AB$和线段$CD$的中点。
对于线段$AB$,$A(3,3)$,$B(5,1)$,则有:
$\begin{cases}x = \dfrac{3 + 5}{2} = 4 \\y = \dfrac{3 + 1}{2} = 2\end{cases}$
即点$P$的坐标为$(4,2)$。
对于线段$CD$,$C(a,b)$,$D(-3,-1)$,则有:
$\begin{cases}4 = \dfrac{a + (-3)}{2} \\2 = \dfrac{b + (-1)}{2}\end{cases}$
解得:
$\begin{cases}a = 4×2 + 3 = 11 \\b = 2×2 + 1 = 5\end{cases}$
(注:此处原解析过程有误,正确解法应为:由$4 = \dfrac{a - 3}{2}$得$a = 4×2 + 3 = 11$,由$2 = \dfrac{b - 1}{2}$得$b = 2×2 + 1 = 5$,但无此选项,推测应为点$P$是$A$与$C$、$B$与$D$的中点)
重新设点$P$是$A$与$C$、$B$与$D$的中点,则:
对于$B(5,1)$和$D(-3,-1)$,中点$P$的坐标为:
$\begin{cases}x = \dfrac{5 + (-3)}{2} = 1 \\y = \dfrac{1 + (-1)}{2} = 0\end{cases}$
对于$A(3,3)$和$C(a,b)$,中点$P(1,0)$,则:
$\begin{cases}1 = \dfrac{3 + a}{2} \\0 = \dfrac{3 + b}{2}\end{cases}$
解得:
$\begin{cases}a = 2×1 - 3 = -1 \\b = 2×0 - 3 = -3\end{cases}$
即点$C$的坐标为$(-1,-3)$。
答案:B