21. (10分)如图,某小区有两个喷泉A,B,两个喷泉的距离为125 m. 现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为60 m,BM的长为75 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)求喷泉B到小路AC的最短距离.
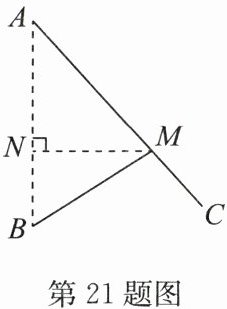
答案:解:
(1)在Rt△MNB中,
∵BM=75m,MN=60m,
∴BN=$\sqrt{75^{2}-60^{2}}$=45(m),
∴AN=AB−BN=125−45=80(m),
∴在Rt△AMN中,AM=$\sqrt{80^{2}+60^{2}}$=100(m).
∴AM+BM=100+75=175(m),
∴供水点M到喷泉A,B需要铺设的管道总长为175m.
(2)
∵AB=125m,AM=100m,BM=75m,
∴$AB^{2}=BM^{2}+AM^{2}$,
∴△ABM是直角三角形,
∴BM⊥AC,
∴喷泉B到小路AC的最短距离是75m.
22. (10分)“儿童散学归来早,忙趁东风放纸鸢”. 又到了放风筝的最佳时节,某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得如图所示的风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米. 求风筝的垂直高度CE.
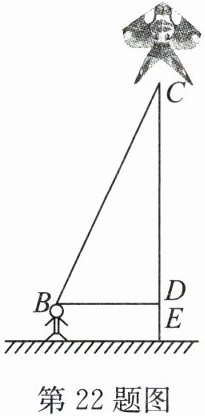
答案:解:在Rt△BCD中,由勾股定理,得$CD^{2}=BC^{2}-BD^{2}=25^{2}-15^{2}=400$,
∴CD=20米.又
∵DE=1.6米,
∴CE=CD+DE=20+1.6=21.6(米).
∴风筝的垂直高度CE为21.6米.
23. (12分)在△ABC中,∠ACB= 90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE= DC.
(1)如图①,延长BC到点F,使得CF= BC,连接AF,EF. 若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②. 若$AB^2= AE^2+BD^2,$用等式表示线段CD与CH之间的数量关系,并说明理由.
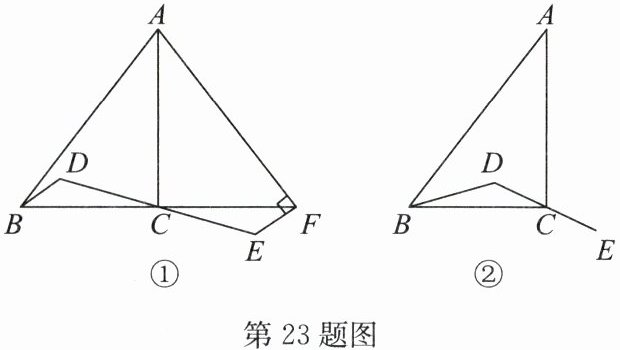
答案:
(1)证明:如答图①,延长BD交AF于点M,
∵AF⊥EF,
∴∠AFE=90°.在△BCD和△FCE中,$\begin{cases} BC=FC, \\ ∠BCD=∠FCE, \\ DC=EC, \end{cases}$
∴△BCD≌△FCE(SAS),
∴∠CBD=∠CFE,
∴BD//EF.
∴∠AMB=∠AFE=90°.
∴BD⊥AF;
(2)解:补全图形如答图②,CH=CD.理由如下:如答图②,延长BC至点F,使CF=BC,连接AF,EF;
∵∠ACB=90°,
∴AC⊥BF,
∴AB=AF;由
(1)可知BH//EF,BD=EF.
∵$AB^{2}=AE^{2}+BD^{2}$,
∴$AF^{2}=AE^{2}+EF^{2}$,
∴∠AEF=90°.
∵BH//EF,
∴∠BHE=90°.又
∵CE=DC,
∴CH=$\frac{1}{2}$DE=CD.