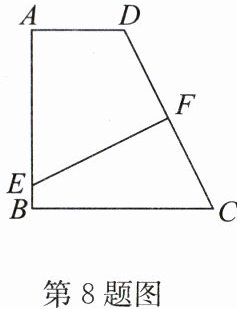
8. 如图,在四边形ABCD中,AD//BC,∠A= 90°,AB= BC= 2AD= 4,边CD的垂直平分线分别交AB,CD于点E,F,则AE的长为(
C
)
A.$\sqrt{13}$
B.7
C.$\frac{7}{2}$
D.$\frac{21}{4}$
解析:
解:设$AE = x$,则$BE = AB - AE = 4 - x$。
过点$D$作$DG \perp BC$于点$G$,
∵$AD // BC$,$\angle A = 90°$,
∴四边形$ABGD$为矩形,
∴$AD = BG$,$AB = DG = 4$。
∵$AB = BC = 4$,$2AD = 4$,
∴$AD = 2$,$BG = 2$,$GC = BC - BG = 4 - 2 = 2$,
∴$D(2, 4)$,$C(4, 0)$(以$B$为原点,$BC$为$x$轴,$BA$为$y$轴建立坐标系)。
∵$EF$垂直平分$CD$,
∴$F$为$CD$中点,$ED = EC$。
$F$点坐标为$\left(\frac{2 + 4}{2}, \frac{4 + 0}{2}\right) = (3, 2)$。
$E$点坐标为$(0, 4 - x)$,
$ED^2 = (2 - 0)^2 + (4 - (4 - x))^2 = 4 + x^2$,
$EC^2 = (4 - 0)^2 + (0 - (4 - x))^2 = 16 + (x - 4)^2$。
∵$ED = EC$,
∴$4 + x^2 = 16 + (x - 4)^2$,
解得$x = \frac{7}{2}$。
答案:C