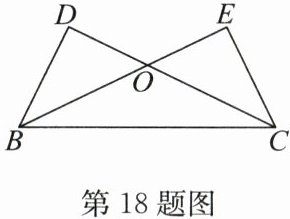
18. (6分)(2024·南京江宁区期末)如图,在$\triangle DBC和\triangle ECB$中,$\angle DBC= \angle ECB$,$\angle EBC= \angle DCB$,$CD与BE交于点O$.求证:$OD = OE$.
答案:证明:在△DBC和△ECB中,{∠DBC=∠ECB,BC=CB,∠DCB=∠EBC,
∴△DBC≌△ECB(ASA).
∴CD=BE.
∵∠EBC=∠DCB,
∴OB=OC.
∴CD - OC=BE - OB,即OD=OE.
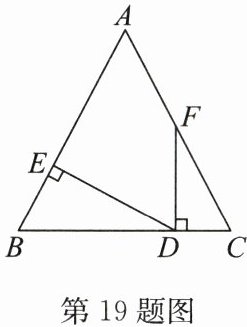
19. (6分)如图,在$\triangle ABC$中,$\angle B= \angle C$,$FD\perp BC$,$DE\perp AB$,$\angle AFD = 152^{\circ}$,求$\angle EDF$的度数.
答案:解:
∵FD⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°.
∵∠AFD=∠C+∠FDC=152°,
∴∠C=152° - ∠FDC=62°.
∵∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=180° - 2×62°=56°.
∵∠A+∠AED+∠EDF+∠AFD=360°,
∴∠EDF=360° - ∠A - ∠AED - ∠AFD=360° - 56° - 90° - 152°=62°.
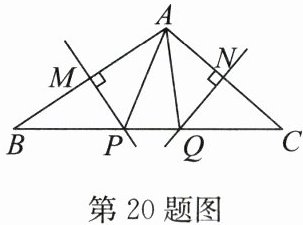
20. (6分)(2024·宿城期末)如图,若$MP和NQ分别垂直平分AB和AC$.
(1)若$\triangle APQ$的周长为12,求$BC$的长;
(2)若$\angle BAC = 105^{\circ}$,求$\angle PAQ$的度数.
答案:
(1)
∵MP和NQ分别垂直平分AB和AC,
∴AP=BP,AQ=CQ.
∴△APQ的周长为AP+PQ+AQ=BP+PQ+CQ=BC.
∵△APQ的周长为12,
∴BC=12.
(2)
∵AP=BP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ.
∵∠BAC=105°,
∴∠BAP+∠CAQ=∠B+∠C=180° - ∠BAC=180° - 105°=75°.
∴∠PAQ=∠BAC - (∠BAP+∠CAQ)=105° - 75°=30°.
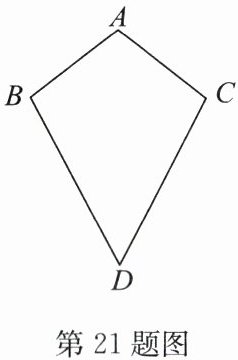
21. (6分)(2024·宿城期中)如图,已知$AB = AC$,$\angle ABD= \angle ACD$.
(1)求证:$BD = CD$;
(2)若连接$AD与BC$,则$AD与BC$有怎样的关系,并说明理由.
答案:(1)证明:如答图①,连接BC.
∵AB=AC,
∴∠ABC=∠ACB.又
∵∠ABD=∠ACD,
∴∠ABD - ∠ABC=∠ACD - ∠ACB,即∠DBC=∠DCB,
∴BD=CD.
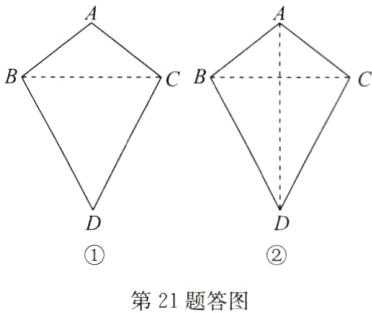
(2)解:如答图②,连接AD,BC.AD垂直平分BC.理由:
∵AB=AC,DB=DC,
∴点A,D都在线段BC的垂直平分线上,
∴AD垂直平分BC.
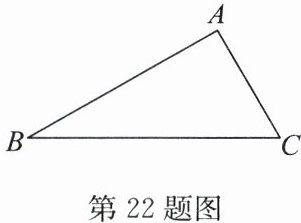
22. (8分)如图,$\triangle ABC$,$AB>AC$.
(1)用尺规求作点$P$,点$P在AB$上,且$PB = PC$;(保留作图痕迹,不写作法)
(2)连接$PC$,若$\angle ACB = 60^{\circ}$,$\angle A = 90^{\circ}$,$AB = 6$,求$PC$的长.
答案:(1)如答图,点P即为所作.
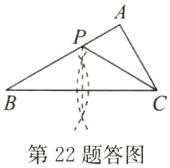
(2)
∵∠ACB=60°,∠A=90°,
∴∠B=30°.
∵PB=PC,
∴∠PCB=∠B=30°,
∴∠ACP=∠ACB - ∠PCB=30°.
∴PC=2PA,即PC=2(6 - PC),
∴PC=4.