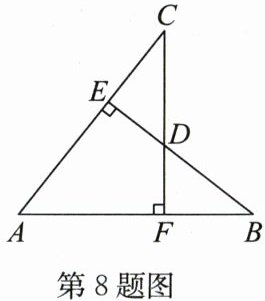
8. (2024·南京秦淮区期末)如图,$AB = AC$,$BE\perp AC$,$CF\perp AB$,垂足分别为$E$,$F$,$CF与BE交于点D$,下列结论:①$\triangle ABE\cong\triangle ACF$;②$\triangle BDF\cong\triangle CDE$;③点$D在\angle BAC$的平分线上;④$AB = DF + DB$.其中所有正确结论的序号是(
C
)
A.①②
B.②③
C.①②③
D.①②③④
答案:C
解析:
证明:
① $\because AB=AC$,$\angle A=\angle A$,$BE\perp AC$,$CF\perp AB$,
$\therefore \angle AEB=\angle AFC=90°$,
$\therefore \triangle ABE \cong \triangle ACF$(AAS),①正确;
② $\because \triangle ABE \cong \triangle ACF$,
$\therefore AE=AF$,$BE=CF$,
$\because AB=AC$,
$\therefore BF=AB-AF=AC-AE=CE$,
$\because \angle BDF=\angle CDE$,$\angle BFD=\angle CED=90°$,
$\therefore \triangle BDF \cong \triangle CDE$(AAS),②正确;
③ 连接$AD$,
$\because \triangle ABE \cong \triangle ACF$,
$\therefore AE=AF$,
$\because AD=AD$,$\angle AED=\angle AFD=90°$,
$\therefore \triangle AED \cong \triangle AFD$(HL),
$\therefore \angle EAD=\angle FAD$,
$\therefore$ 点$D$在$\angle BAC$的平分线上,③正确;
④ $\because \triangle BDF \cong \triangle CDE$,
$\therefore DF=DE$,$DB=DC$,
$\because BE=BD+DE=BD+DF$,但$BE \neq AB$,
$\therefore AB \neq DF+DB$,④错误.
综上,正确结论的序号是①②③.
答案:C
9. (2024·宿城期中)在$\triangle ABC$中,$\angle A = 45^{\circ}$,$\angle B = 60^{\circ}$.若$\triangle ABC\cong\triangle DEF$,则$\angle F$的度数为
75°
.
答案:75°
解析:
在$\triangle ABC$中,$\angle A + \angle B + \angle C = 180°$,$\angle A = 45°$,$\angle B = 60°$,则$\angle C = 180° - 45° - 60° = 75°$。
因为$\triangle ABC \cong \triangle DEF$,所以$\angle F = \angle C = 75°$。
$75°$
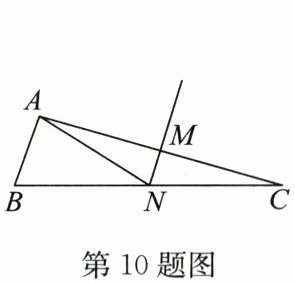
10. (2024·宿城期中)如图,在$\triangle ABC$中,边$AC的垂直平分线交AC于点M$,交$BC于点N$.若$AB = 3$,$BC = 13$,则$\triangle ABN$的周长是
16
.
答案:16
解析:
解:
∵MN是AC的垂直平分线,
∴AN=CN,
∵BC=13,
∴BN+CN=BN+AN=13,
∵AB=3,
∴△ABN的周长=AB+BN+AN=3+13=16.
16
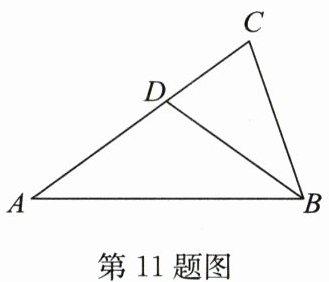
11. (2024·重庆B卷)如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,$BD平分\angle ABC交AC于点D$.若$BC = 2$,则$AD$的长为______.
2
答案:2
解析:
解:
∵ $AB = AC$,$\angle A = 36°$,
∴ $\angle ABC = \angle C = \frac{180° - 36°}{2} = 72°$。
∵ $BD$ 平分 $\angle ABC$,
∴ $\angle ABD = \angle DBC = \frac{72°}{2} = 36°$。
∴ $\angle BDC = 180° - \angle DBC - \angle C = 180° - 36° - 72° = 72°$。
∵ $\angle BDC = \angle C$,$\angle A = \angle ABD$,
∴ $AD = BD$,$BD = BC$。
∵ $BC = 2$,
∴ $AD = BD = BC = 2$。
2
12. 等腰三角形的一个内角为$50^{\circ}$,那么这个等腰三角形的一个底角的度数为
50°或65°
.
答案:50°或65°
解析:
当$50^{\circ}$角为顶角时,底角的度数为$\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$;
当$50^{\circ}$角为底角时,底角的度数为$50^{\circ}$。
$50^{\circ}$或$65^{\circ}$
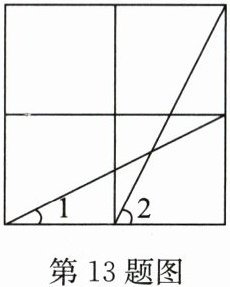
13. 如图,已知方格纸中是4个相同的小正方形,则$\angle 1+\angle 2$的度数为
90°
.
答案:90°
解析:
设每个小正方形的边长为1。
在方格纸中,∠1所在的直角三角形两直角边分别为1、2,∠2所在的直角三角形两直角边分别为1、2,易证这两个三角形全等,故对应角相等。
∠1的余角与∠2相等,因此∠1+∠2=90°。
90°
14. 如图,在$\triangle ABC$中,$\angle CAD= \angle EAD$,$\angle ADC= \angle ADE$,$CB = 5\mathrm{cm}$,$BD = 3\mathrm{cm}$,则$ED$的长为
2
$\mathrm{cm}$.
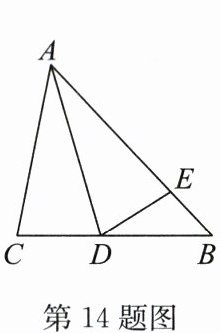
答案:2
解析:
证明:在$\triangle ADC$和$\triangle ADE$中,
$\left\{\begin{array}{l}\angle CAD = \angle EAD \\AD = AD \\\angle ADC = \angle ADE\end{array}\right.$
$\therefore \triangle ADC \cong \triangle ADE(ASA)$
$\therefore DC = DE$
$\because CB = 5\mathrm{cm}$,$BD = 3\mathrm{cm}$
$\therefore DC = CB - BD = 5 - 3 = 2\mathrm{cm}$
$\therefore ED = DC = 2\mathrm{cm}$
2
15. (2024·南京浦口区期末)如图,等边$\triangle ABC$中,$AD是BC$边上的中线,且$AD = 17$,$E$,$P分别是AC$,$AD$上的动点,则$CP + EP$的最小值等于
17
.
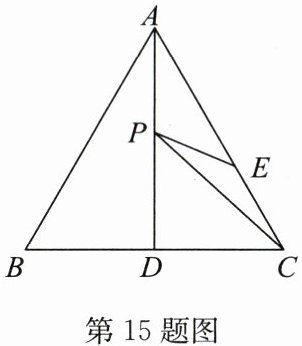
答案:17
解析:
证明:
∵△ABC是等边三角形,AD是BC边上的中线,
∴AD垂直平分BC,B、C关于AD对称。
作点C关于AD的对称点B,连接BE交AD于点P,此时CP+EP=BP+EP=BE最小。
当BE⊥AC时,BE的值最小。
∵△ABC是等边三角形,
∴BE=AD=17(等边三角形三线合一)。
故CP+EP的最小值为17。
17
16. 如图,在等腰直角三角形$ABC$中,$\angle BAC = 90^{\circ}$,$D是AC$的中点,$CE\perp BD于点E$,交$BA的延长线于点F$,若$BF = 12$,则$\triangle FBC$的面积为
48
.
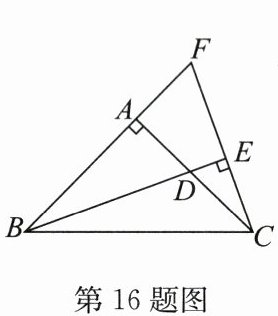
答案:48
解析:
证明:
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AB=AC,∠BAD=∠CAF=90°.
∵CE⊥BD,
∴∠BEC=90°,
∴∠ABD+∠F=90°,∠ACF+∠F=90°,
∴∠ABD=∠ACF.
在△ABD和△ACF中,
$\left\{\begin{array}{l} ∠BAD=∠CAF, \\ AB=AC, \\ ∠ABD=∠ACF, \end{array}\right.$
∴△ABD≌△ACF(ASA),
∴AD=AF.
∵D是AC中点,
∴AD=$\frac{1}{2}$AC=$\frac{1}{2}$AB,
∴AF=$\frac{1}{2}$AB.设AB=AC=x,则AF=$\frac{1}{2}$x.
∵BF=BA+AF=x+$\frac{1}{2}$x=12,解得x=8,即AB=AC=8.
∴△FBC的面积=$\frac{1}{2}$×BF×AC=$\frac{1}{2}$×12×8=48.
48
17. (6分)如图,点$E$,$F在线段CD$上,且$CE = DF$,$AE = BF$,$AE// BF$.求证:$\triangle AEC\cong\triangle BFD$.
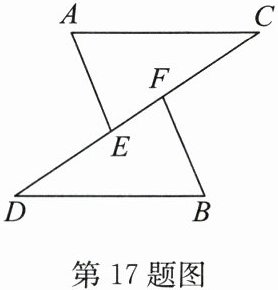
答案:证明:
∵AE//BF,
∴∠AEC=∠BFD.又
∵CE=DF,AE=BF,
∴△AEC≌△BFD(SAS).