1. 全等三角形是指两个三角形(
A
)
A.能够完全重合
B.形状相同
C.面积相等
D.周长相等
答案:A
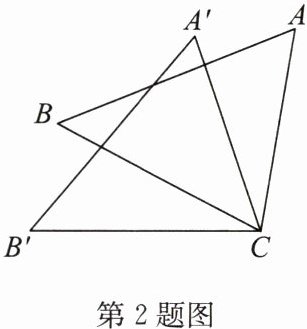
2. 如图,$\triangle ACB\cong\triangle A'CB'$,若$\angle B = 50^{\circ}$,则$\angle B'$的度数为(
D
)
A.$20^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$50^{\circ}$
答案:D
解析:
证明:
∵$\triangle ACB\cong\triangle A'CB'$,
∴$\angle B=\angle B'$(全等三角形对应角相等)。
∵$\angle B = 50^{\circ}$,
∴$\angle B'=50^{\circ}$。
D
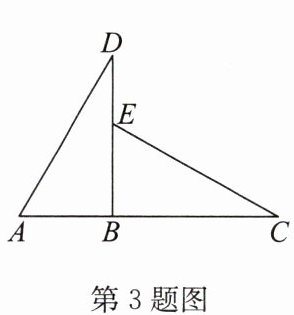
3. 如图,$\triangle ABD\cong\triangle EBC$,$AB = 4\mathrm{cm}$,$BC = 7\mathrm{cm}$,则$DE = $
3
$\mathrm{cm}$。
答案:3
解析:
解:
∵△ABD≌△EBC,
∴AB=EB=4cm,BD=BC=7cm,
∵DE=BD-EB,
∴DE=7-4=3cm。
3
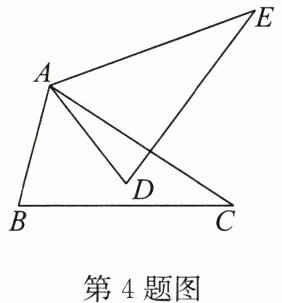
4. 如图,$\triangle ABC\cong\triangle ADE$,$\angle C = 35^{\circ}$,$\angle D = 75^{\circ}$,则$\angle DAE = $
70°
。
答案:70°
解析:
证明:
∵$\triangle ABC\cong\triangle ADE$,
∴$\angle B=\angle D=75°$,$\angle E=\angle C=35°$。
在$\triangle ADE$中,$\angle DAE+\angle D+\angle E=180°$,
∴$\angle DAE=180°-\angle D-\angle E=180°-75°-35°=70°$。
$70°$
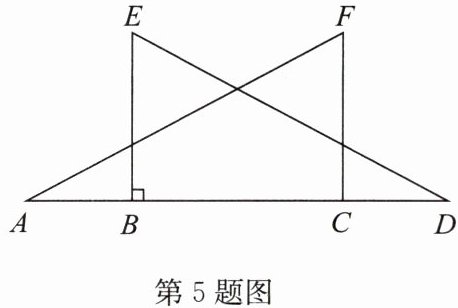
5. 如图,$\triangle ACF\cong\triangle DBE$,其中点$A$,$B$,$C$,$D$在一条直线上。
(1) 若$BE\perp AD$,$\angle F = 62^{\circ}$,求$\angle A$的度数;
(2) 若$AD = 9\mathrm{cm}$,$BC = 5\mathrm{cm}$,求$AB$的长。
答案:
(1)
∵BE⊥AD,
∴∠EBD=90°.
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°−∠F=28°.
(2)
∵△ACF≌△DBE,
∴CA=BD,
∴CA−CB=BD−BC,即AB=CD,
∵AD=9cm,BC=5cm,
∴AB+CD=9−5=4(cm),
∴AB=2cm.
6. 如图,若点$D在边BC$上,$\triangle ABC\cong\triangle ADE$,则下列结论中不一定成立的是(
D
)
A.$AB = AD$
B.$DE = BC$
C.$\angle ADB = \angle ADE$
D.$\angle ACD = \angle CAD$
答案:D
解析:
证明:
∵$\triangle ABC\cong\triangle ADE$,
∴$AB=AD$(A成立),$DE=BC$(B成立),$\angle ADE=\angle B$。
∵$\angle ADB=\angle B+\angle BAD$,$\angle ADE=\angle B$,
∴$\angle ADB=\angle ADE+\angle BAD$,即$\angle ADB>\angle ADE$(C不成立)。
$\angle ACD$与$\angle CAD$大小关系不确定(D不一定成立)。
结论:不一定成立的是D。
D
7. 一个三角形的三边长分别为$3$,$5$,$x$,另一个三角形的三边长分别为$y$,$3$,$6$。若这两个三角形全等,则$x + y = $
11
。
答案:11
解析:
因为两个三角形全等,全等三角形的对应边相等。
第一个三角形的三边长为$3$,$5$,$x$;第二个三角形的三边长为$y$,$3$,$6$。
两个三角形中都有边长为$3$的边,所以$3$是对应边。
则剩下的边应分别对应相等,所以$x = 6$,$y = 5$。
因此$x + y=6 + 5=11$。
11