7. 如图,在 $ \triangle ABC $ 中,$ \angle 1 = \angle 2 = \angle 3 = \angle 4 $. 下列说法中,正确的是(
B
)
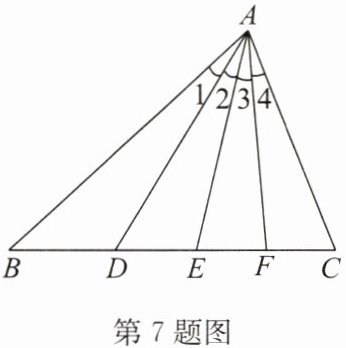
A.$ AD $ 是 $ \triangle ABE $ 的中线
B.$ AE $ 是 $ \triangle ABC $ 的角平分线
C.$ AF $ 是 $ \triangle ACE $ 的高线
D.$ AE $ 是 $ \triangle ABC $ 的中线
答案:B
解析:
∵∠1=∠2=∠3=∠4,
∴∠BAE=∠1+∠2=2∠1,∠EAC=∠3+∠4=2∠1,
∴∠BAE=∠EAC,
∴AE是△ABC的角平分线。
B
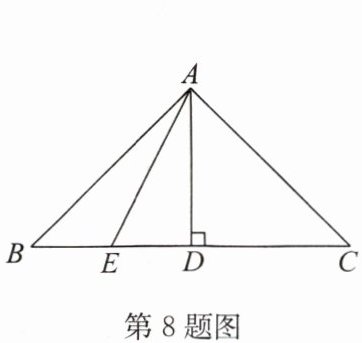
8. 如图,$ AD $ 是 $ \triangle ABC $ 的中线,也是 $ \triangle ABC $ 的高,$ AE $ 是 $ \triangle ABD $ 的中线,若 $ \triangle ABE $ 的面积为 $ 4 $,$ BC = 8 $,则 $ AD = $
4
.
答案:4
解析:
解:
∵AD是△ABC的中线,BC=8,
∴BD=DC=$\frac{1}{2}$BC=4.
∵AD是△ABC的高,
∴S△ABD=S△ADC=$\frac{1}{2}$S△ABC.
∵AE是△ABD的中线,
∴BE=ED=$\frac{1}{2}$BD,
∴S△ABE=S△AED=$\frac{1}{2}$S△ABD.
∵S△ABE=4,
∴S△ABD=2×4=8.
又
∵S△ABD=$\frac{1}{2}$×BD×AD,BD=4,
∴8=$\frac{1}{2}$×4×AD,
解得AD=4.
4
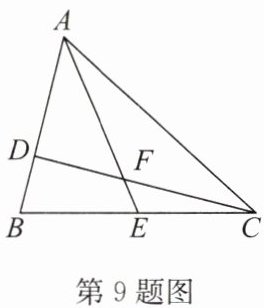
9. (2024·宿城期中)如图,$ D $,$ E $ 分别是 $ \triangle ABC $ 的边 $ AB $、$ BC $ 上的点,$ AD = 2BD $,$ BE = CE $,设 $ \triangle ADF $ 的面积为 $ S_1 $,$ \triangle CEF $ 的面积为 $ S_2 $. 若 $ S_{\triangle ABC} = 12 $,则 $ S_1 - S_2 $ 的值为______.
2
答案:2
解析:
解:设$S_{\triangle BDF}=x$,$S_{\triangle BEF}=y$。
因为$AD = 2BD$,$S_{\triangle ABC}=12$,所以$S_{\triangle BCD}=\frac{1}{3}S_{\triangle ABC}=4$,$S_{\triangle ACD}=\frac{2}{3}S_{\triangle ABC}=8$。
因为$BE = CE$,所以$S_{\triangle ABE}=S_{\triangle ACE}=6$,$S_{\triangle BDE}=S_{\triangle CDE}$,即$x + y = S_2$。
$S_{\triangle ADF}=S_{\triangle ABE}-S_{\triangle BDF}-S_{\triangle BEF}=6 - x - y$,即$S_1=6 - x - y$。
$S_{\triangle CDE}=S_{\triangle BCD}-S_{\triangle BDE}=4 - (x + y)$,又$S_{\triangle CDE}=S_2$,所以$S_2=4 - x - y$。
$S_1 - S_2=(6 - x - y)-(4 - x - y)=2$。
2
10. 如图,在 $ \triangle ABC $ 中 ($ AB > BC $),$ AB = 2AC $,$ AC $ 边上的中线 $ BD $ 把 $ \triangle ABC $ 的周长分成 $ 30 $ 和 $ 20 $ 两部分,求 $ AB $ 和 $ BC $ 的长.
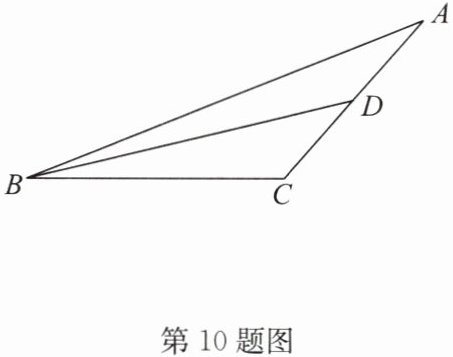
答案:解:设AC=x,则AB=2x.因为BD是中线,
所以AD=CD=$\frac{1}{2}x$.
由题意,得2x+$\frac{1}{2}x$=30,解得x=12,
则AC=12,AB=24,CD=6,
所以BC=20−CD=20−6=14.
11. 如图,在 $ \triangle ABC $ 中,$ \angle BAC = 90^{\circ} $,$ BE $ 是角平分线,$ AD $ 是高,$ BE $,$ AD $ 相交于点 $ F $. 试说明:$ \angle 1 = \angle 2 $.
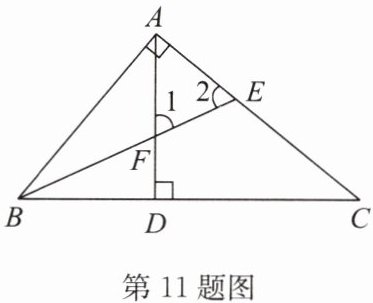
答案:解:因为BE是角平分线,
所以∠ABE=∠CBE.
因为∠BAC=90°,
所以∠ABE+∠2=90°.
因为AD是高,所以∠CBE+∠BFD=90°.
所以∠2=∠BFD
又因为∠1=∠BFD,所以∠1=∠2.
12. (2024·宿豫期中)如图,$ AD $ 是 $ \triangle ABC $ 的高,$ CE $ 是 $ \angle ACB $ 的平分线,$ \angle 1 = \angle B $,$ \angle ACB = 66^{\circ} $.
(1) 求 $ \angle BAC $ 的度数;
(2)
钝角
$ \triangle AFC $ 是______三角形(按角分类),写出理由.
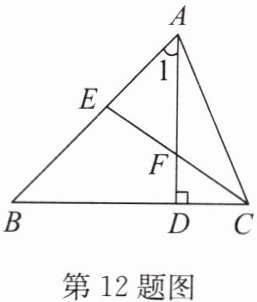
答案:
(1)
∵AD是△ABC的高,
∴∠ADB=90°.
∵∠1=∠B,
∴∠1=∠B=$\frac{180^{\circ}-\angle ADB}{2}$=45°.
∵∠ACB=66°,
∴∠BAC=180°−∠B−∠ACB=69°.
(2)钝角 理由如下:
∵AD是△ABC的高,CE是∠ACB的平分线,
∴∠CDF=90°,∠DCF=$\frac{1}{2}$∠ACB=33°,
∴∠AFC=∠CDF+∠DCF=123°.
∴△AFC是钝角三角形.