8. 在△ABC中,$∠A = 50^{\circ}$,当$∠B = $
50°或65°或80°
时,△ABC是等腰三角形.
答案:50°或65°或80°
解析:
当∠A为顶角时,∠B=∠C,∠B=(180°-50°)/2=65°;
当∠A为底角,∠B为顶角时,∠B=180°-2×50°=80°;
当∠A为底角,∠B为底角时,∠B=∠A=50°.
50°或65°或80°
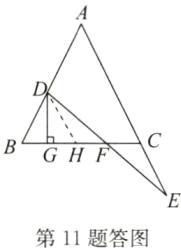
9. 如图,AD是△ABC的角平分线,$CE// AD$,与BA的延长线相交于点E,点F在AD的延长线上,且$FC = AC$. 求证:(1)△ACE是等腰三角形;(2)$AB// CF$.
答案:证明:
(1)
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∵CE//AD,
∴∠BAD=∠E,∠CAD=∠ACE,
∴∠E=∠ACE,
∴AC=AE,即△ACE是等腰三角形.
(2)
∵FC=AC,
∴∠F=∠DAC.又
∵∠BAD=∠DAC,
∴∠F=∠BAD,
∴AB//CF.
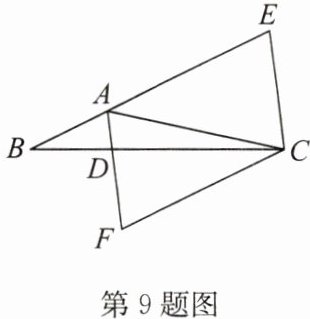
10. (2024·自贡)如图,在△ABC中,$DE// BC$,$∠EDF = ∠C$.
(1)求证:$∠BDF = ∠A$;
(2)若$∠A = 45^{\circ}$,DF平分$∠BDE$,请求出△ABC的形状.
答案:
(1)证明:
∵DE//BC,
∴∠C=∠AED.
∵∠EDF=∠C,
∴∠AED=∠EDF,
∴DF//AC,
∴∠BDF=∠A.
(2)解:
∵∠A=45°,
∴∠BDF=45°.
∵DF平分∠BDE,
∴∠BDE=2∠BDF=90°.
∵DE//BC,
∴∠B=180° - ∠BDE=90°.又∠A=45°,
∴△ABC是等腰直角三角形.
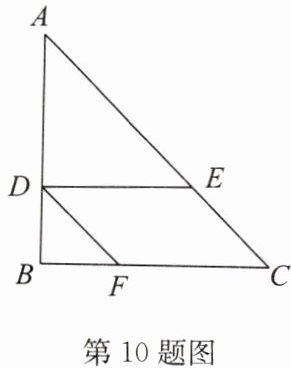
11. 如图,在△ABC中,$AB = AC$,点D在AB边上,点E在AC的延长线上,且$CE = BD$,连接DE交BC于点F.
(1)求证:$EF = DF$;
(2)过点D作$DG⊥BC$,垂足为G,求证:$BC = 2FG$.
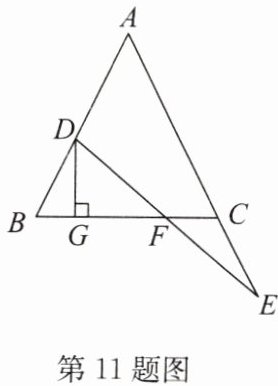
答案:证明:
(1)过点D作DH//AC,交BC于点H,如答图,则∠DHB=∠ACB,∠DHF=∠ECF.
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DHB,
∴BD=HD.
∵CE=BD,
∴HD=CE.在△DHF和△ECF中,∠DHF=∠ECF,∠DFH=∠EFC,HD=CE,
∴△DHF≌△ECF(AAS).
∴EF=DF.
(2)由
(1)知BD=HD.
∵DG⊥BC,
∴BG=GH,由
(1)得△DHF≌△ECF,
∴HF=CF,
∴FG=GH+HF=$\frac{1}{2}$BH+$\frac{1}{2}$CH=$\frac{1}{2}$BC,
∴BC=2FG.