7. 已知C,D两点在线段AB的垂直平分线上,且∠ACB= 50°,∠ADB= 90°,则∠CAD=
110°或20°
.
答案:110°或20°
解析:
∵C,D两点在线段AB的垂直平分线上
∴CA=CB,DA=DB
∴△CAB,△DAB均为等腰三角形
设AB的垂直平分线交AB于点O
情况1:C,D在AB同侧
∵∠ACB=50°
∴∠CAB=(180°-50°)/2=65°
∵∠ADB=90°
∴∠DAB=(180°-90°)/2=45°
∴∠CAD=∠CAB-∠DAB=65°-45°=20°
情况2:C,D在AB异侧
∠CAD=∠CAB+∠DAB=65°+45°=110°
20°或110°
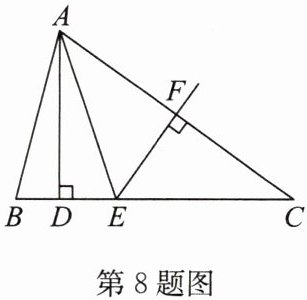
8. (2024·湖滨新区期末)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD= DE,连接AE.
(1)若∠BAE= 40°,求∠C的度数;
(2)若△ABC的周长为20 cm,AC= 8 cm,求DC的长.
答案:解:
(1)
∵AD⊥BC,BD=DE,
∴AD垂直平分线段BE,
∴AB=AE,
∴∠B=∠AEB.
∵∠BAE=40°,
∴∠AEB= $\frac{1}{2}(180° - ∠BAE)=70°$.
∵EF垂直平分AC,
∴EA=EC,
∴∠C=∠EAC.又
∵∠AEB=∠EAC + ∠C,
∴∠C= $\frac{1}{2}∠AEB=35°$.
(2)
∵△ABC的周长为20 cm,AC=8 cm,
∴AB + BC=12 cm.
∵AB=AE=CE,BD=DE,
∴CE + DE= $\frac{1}{2}(AB + BC)=6$ cm,即DC=6 cm.
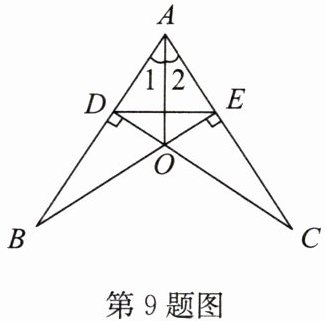
9. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,连接DE,BE与CD交于点O,OB= OC.
求证:(1)∠1= ∠2;
(2)直线AO垂直平分线段DE.
答案:证明:
(1)
∵CD⊥AB,BE⊥AC,
∴∠ODB=∠OEC=∠ODA=∠OEA=90°.又
∵∠BOD=∠COE,OB=OC,
∴△BOD≌△COE(AAS).
∴OD=OE.又
∵OA=OA,
∴Rt△AOD≌Rt△AOE(HL).
∴∠1=∠2,AD=AE.
(2)
∵OD=OE,AD=AE,
∴点A和点O都在线段DE的垂直平分线上.又
∵两点确定一条直线,
∴直线AO垂直平分线段DE.
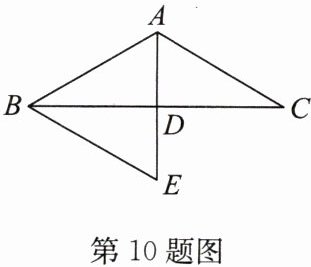
10. (2024·南充)如图,在△ABC中,D为BC边的中点,过点B作BE//AC交AD的延长线于点E.
(1)求证:△BDE≌△CDA;
(2)若AD⊥BC,求证:BA= BE.
答案:证明:
(1)
∵D为BC的中点,
∴BD=CD.
∵BE//AC,
∴∠EBD=∠C,∠E=∠CAD.在△BDE和△CDA中,$\left\{\begin{array}{l}∠EBD=∠C,\\∠E=∠CAD,\\BD=CD,\end{array}\right.$
∴△BDE≌△CDA(AAS).
(2)
∵D为BC的中点,AD⊥BC,
∴直线AD为线段BC的垂直平分线,
∴BA=CA.由
(1)可知△BDE≌△CDA,
∴BE=CA,
∴BA=BE.